题目内容
已知椭圆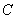 的方程为
的方程为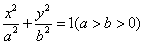 ,点
,点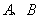 分别为其左、右顶点,点
分别为其左、右顶点,点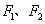 分别为其左、右焦点,以点
分别为其左、右焦点,以点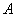 为圆心,
为圆心,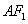 为半径作圆
为半径作圆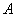 ;以点
;以点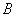 为圆心,
为圆心,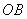 为半径作圆
为半径作圆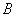 ;若直线
;若直线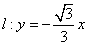 被圆
被圆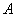 和圆
和圆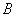 截得的弦长之比为
截得的弦长之比为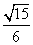 ;
;
(1)求椭圆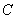 的离心率;
的离心率;
(2)己知a=7,问是否存在点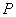 ,使得过
,使得过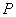 点有无数条直线被圆
点有无数条直线被圆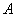 和圆
和圆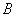 截得的弦长之比为
截得的弦长之比为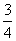 ;若存在,请求出所有的
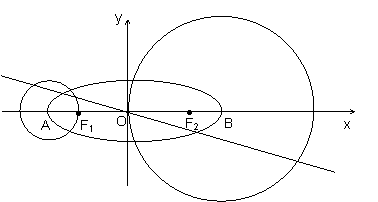
;若存在,请求出所有的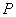 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.

【答案】(1)由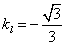 ,得直线
,得直线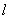 的倾斜角为
的倾斜角为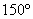 ,
,
则点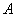 到直线
到直线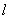 的距离
的距离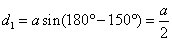 ,
,
故直线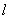 被圆
被圆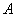 截得的弦长为
截得的弦长为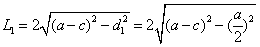 ,
,
直线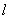 被圆
被圆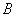 截得的弦长为
截得的弦长为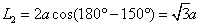 ,
,
据题意有: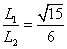 ,即
,即 ,
,
化简得: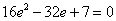 ,
,
解得: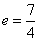 或
或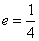 ,又椭圆的离心率
,又椭圆的离心率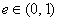 ;
;
故椭圆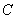 的离心率为
的离心率为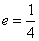 .
.
(2)假设存在,设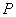 点坐标为
点坐标为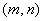 ,过
,过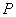 点的直线为
点的直线为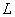 ;
;
当直线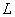 的斜率不存在时,直线
的斜率不存在时,直线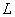 不能被两圆同时所截;
不能被两圆同时所截;
故可设直线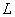 的方程为
的方程为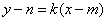 ,
,
则点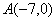 到直线
到直线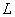 的距离
的距离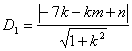 ,
,
由(1)有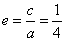 ,得
,得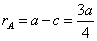 =
=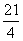 ,
,
故直线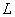 被圆
被圆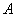 截得的弦长为
截得的弦长为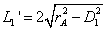 ,
,
则点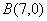 到直线
到直线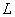 的距离
的距离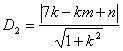 ,
,
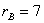 ,故直线
,故直线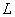 被圆
被圆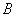 截得的弦长为
截得的弦长为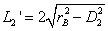 ,
,
据题意有: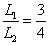 ,即有
,即有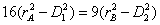 ,整理得
,整理得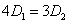 ,
,
即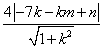
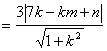 ,
,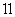
所以4|―7k―km+n|=3|7k-km+n|,
即4(―7k―km+n)=3(7k-km+n)或4(―7k―km+n)=-3(7k-km+n),
也就是(49+m)k-n=0或(1+m)k-n=0与k无关.
于是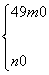 或
或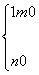 ,
,
故所求点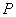 坐标为(-1,0)或(-49,0).
坐标为(-1,0)或(-49,0).
方法二 对式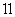 两边平方整理成关于
两边平方整理成关于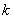 的一元二次方程得
的一元二次方程得
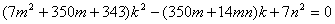 ,
,
关于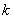 的方程有无穷多解,
的方程有无穷多解,
故有: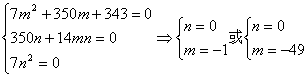 ,
,
故所求点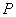 坐标为(-1,0)或(-49,0).
坐标为(-1,0)或(-49,0).
(注设过P点的直线为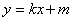 后求得P点坐标同样得分)
后求得P点坐标同样得分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
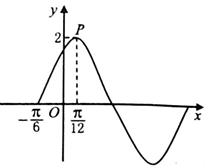
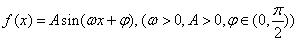 . 的部分图象如图所示,其中点P是图象的一个最高点。
. 的部分图象如图所示,其中点P是图象的一个最高点。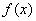 的解析式;
的解析式;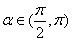 且
且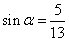 ,求
,求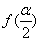 .
.
 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 的最大值为8,则a+b的最小值为_____________.
的最大值为8,则a+b的最小值为_____________.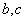 表示两条直线,
表示两条直线,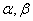 表示两个平面,现给出下列命题:
表示两个平面,现给出下列命题: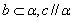 ,则
,则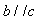 ; ② 若
; ② 若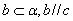 ,则
,则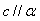 ;
;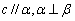 ,则
,则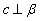 ; ④ 若
; ④ 若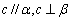 ,则
,则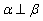 .
.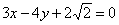 与抛物线
与抛物线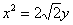 和圆
和圆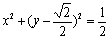 从左到右的交点依次为
从左到右的交点依次为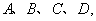 则
则 的值为 .
的值为 . 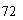 ,半径
,半径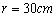 ,则扇形的周长为
,则扇形的周长为  。
。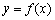 是定义在
是定义在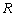 上的奇函数,且当
上的奇函数,且当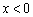 时,
时,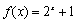 ,则
,则 。
。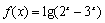 的定义域为 .
的定义域为 . ,求满足
,求满足 且在圆
且在圆
 上的点
上的点 的坐标
的坐标