题目内容
3.在极坐标系中,点$(2,\frac{π}{3})$与点(1,0)的距离为( )| A. | 2 | B. | $\sqrt{4+\frac{π^2}{9}}$ | C. | $\sqrt{1+\frac{π^2}{9}}$ | D. | $\sqrt{3}$ |
分析 点$(2,\frac{π}{3})$化为直角坐标:(1,$\sqrt{3}$),利用两点之间的距离公式即可得出.
解答 解:点$(2,\frac{π}{3})$化为直角坐标:(1,$\sqrt{3}$),
∴两点之间的距离d=$\sqrt{(1-1)^{2}+(\sqrt{3})^{2}}$=$\sqrt{3}$.
故选:D.
点评 本题考查了极坐标化为直角坐标、两点之间的距离公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
4.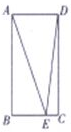 在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )
在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )
 在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )
在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )| A. | 12 | B. | 15 | C. | 17 | D. | 16 |
11.若P(2,1)为圆(x-1)2+y2=25的弦AB的中点,则直线AB的方程为( )
| A. | 2x+y-3=0 | B. | x+y-1=0 | C. | x+y-3=0 | D. | 2x-y-5=0 |
12.已知圆锥的底面半径为2,且它的侧面展开图是一个半圆,则这个圆锥的表面积为( )
| A. | 8π | B. | 12π | C. | 4π | D. | 10π |
13.齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现从双方的马匹中随机选一匹进行一场比赛,则在齐王的马获胜的条件下,齐王的上等马获胜的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 1 |