题目内容
11.sin1cos2tan3的值为( )| A. | 负数 | B. | 正数 | C. | 0 | D. | 不存在 |
分析 根据正弦余弦和正切的角象限的正负判断即可.
解答 解:由题意:要是判断sin1cos2tan3的值的正负:
∵$0<1<\frac{π}{2}$,
∴sin1>0;
∵$\frac{π}{2}<2<π$,$\frac{π}{2}<3<π$
∴cos2<0;tan3<0.
所以sin1cos2tan3>0.
故选:B.
点评 本题考查了正弦余弦和正切的角象限的正负的判断及运用.比较基础.

练习册系列答案
相关题目
6.用五点作图法作y=2sin4x的图象时,首先描出的五个点的横坐标是( )
| A. | 0,$\frac{π}{2}$,π,$\frac{3π}{2}$,2π | B. | 0,$\frac{π}{4}$,$\frac{π}{2}$,$\frac{3π}{4}$,π | C. | 0,$\frac{π}{8}$,$\frac{π}{4}$,$\frac{3π}{8}$,$\frac{π}{2}$ | D. | 0,$\frac{π}{6}$,$\frac{π}{3}$,$\frac{3π}{2}$,$\frac{2}{3}$π |
16.已知函数f(x)=cos(2x+φ),|φ|≤$\frac{π}{2}$,若f($\frac{8π}{3}$-x)=-f(x),则要得到y=sin2x的图象只需将y=f(x)的图象( )
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
3.函数$f(x)=\sqrt{x({3-x})}+\sqrt{x-1}$的定义域为( )
| A. | {x|0≤x≤3} | B. | {x|1≤x≤3} | C. | {x|x≥1} | D. | {x|x≥3} |
12.函数f(x)=$\left\{\begin{array}{l}{x+1(x≥0)}\\{{x}^{2}+2x+1(x<0)}\end{array}\right.$,若矩形ABCD的顶点A、D在x轴上,B、C在函数y=f(x)的图象上,且A(1,0),则点D的坐标为( )
| A. | (-2,0) | B. | (-1-$\sqrt{2}$,0) | C. | (-1,0) | D. | (-$\frac{1}{2}$,0) |
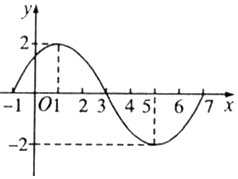 已知函数y=Asin(ωx+φ)(A>0,ω>0)在一个周期内的图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0)在一个周期内的图象如图所示.