题目内容
在平面直角坐标系xOy中,已知椭圆C1: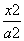 +
+ =1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
=1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
(1)求椭圆C1的方程;
(2)设直线l同时与椭圆C1和抛物线C2:y2=4x相切,求直线l的方程.
解 (1)因为椭圆C1的左焦点为F1(-1,0),所以c=1.
把点P(0,1)代入椭圆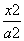 +
+ =1,得
=1,得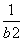 =1,即b=1,
=1,即b=1,
所以a2=b2+c2=2.
所以椭圆C1的方程为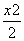 +y2=1.
+y2=1.
(2)由题意可知,直线l的斜率显然存在,且不等于0,设直线l的方程为y=kx+m.
联立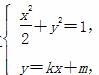 消去y并整理得
消去y并整理得
(1+2k2)x2+4kmx+2m2-2=0.
因为直线l与椭圆C1相切,
所以Δ1=16k2m2-4(1+2k2)(2m2-2)=0,
整理得2k2-m2+1=0.①
联立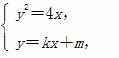
消去y并整理得k2x2+(2km-4)x+m2=0.
因为直线l与抛物线C2相切,
所以Δ2=(2km-4)2-4k2m2=0.
整理得km=1.②
综合①②,解得 或
或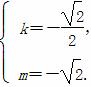
所以直线l的方程为y=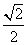 x+
x+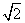 或y=-
或y=-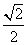 x-
x-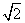 .
.

练习册系列答案
相关题目
 -
- =1的一个焦点是(0,2),椭圆
=1的一个焦点是(0,2),椭圆 -
-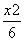 -
-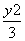 =1的右焦点为圆心且与双曲线的渐近线相切的圆的方程是( ).
=1的右焦点为圆心且与双曲线的渐近线相切的圆的方程是( ). )2+y2=
)2+y2= -
-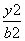 =1(a>0,b>0)的左、右焦点分别为F1和F2,线段F1F2被抛物线y2=2bx的焦点分成5∶3两段,则此双曲线的离心率为________.
=1(a>0,b>0)的左、右焦点分别为F1和F2,线段F1F2被抛物线y2=2bx的焦点分成5∶3两段,则此双曲线的离心率为________.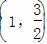 且离心率为
且离心率为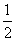 .
.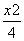 -y2=1相交于A,B两点,则|AB|的最小值为( ).
-y2=1相交于A,B两点,则|AB|的最小值为( ).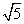 C.4 D.2
C.4 D.2 和
和 表示的点关于虚轴对称,则复数
表示的点关于虚轴对称,则复数 ( )
( ) B.
B. C.
C.  D.
D. 
 满足
满足 ,
, (
( )。
)。 为等比数列,并求数列
为等比数列,并求数列 的通项公式;
的通项公式; ,求
,求 的前n项和
的前n项和 ;
; ,数列
,数列 的前n项和
的前n项和 ,求证:对
,求证:对 。
。