题目内容
某农场计划种植甲、乙两个品种的蔬菜,总面积不超过300亩,总成本不超过9万元.甲、乙两种蔬菜的成本分别是每亩600元和每亩200元.假设种植这两个品种的蔬菜,能为该农场带来的收益分别为每亩0.3万元和每亩0.2万元.问该农场如何分配甲、乙两种蔬菜的种植面积,可使农场的总收益最大,最大收益是多少万元?
考点:简单线性规划
专题:不等式的解法及应用
分析:设甲、乙两种蔬菜的种植面积分别为x,y亩,农场的总收益为z万元,建立目标函数和约束条件,利用线性规划进行求解即可.
解答:
解:设甲、乙两种蔬菜的种植面积分别为x,y亩,农场的总收益为z万元,则…(1分)
…①…(5分)
目标函数为z=0.3x+0.2y,…(6分)
不等式组①等价于
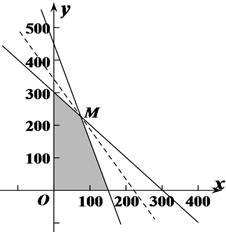
可行域如图所示,…(9分)
当目标函数对应的直线经过点M时,
目标函数z取最小值.…(10分)
解方程组
得M的坐标(75,225)…(12分)
所以zmax=0.3×75+0.2×225=67.5.…(13分)
答:分别种植甲乙两种蔬菜75亩和225亩,可使农场的总收益最大,最大收益为67.5万元.
…(14分)
|
目标函数为z=0.3x+0.2y,…(6分)
不等式组①等价于
|

可行域如图所示,…(9分)
当目标函数对应的直线经过点M时,
目标函数z取最小值.…(10分)
解方程组
|
得M的坐标(75,225)…(12分)
所以zmax=0.3×75+0.2×225=67.5.…(13分)
答:分别种植甲乙两种蔬菜75亩和225亩,可使农场的总收益最大,最大收益为67.5万元.
…(14分)
点评:本题主要考查线性规划的应用问题,根据条件建立约束条件,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
以下条件表达式正确的是( )
| A、1<x<2 | B、x><1 |
| C、x<>1 | D、x≤1 |
为了了解学生对新课程改革的满意情况,有关教育部门对某中学的100名学生随机进行了调查,得到如下的统计表:
已知在全部100名学生中随机抽取1人对课程改革满意的概率为
.参照附表,得到的正确结论是( )
| 满 意 | 不满意 | 合 计 | |
| 男 生 | 50 | ||
| 女 生 | 15 | ||
| 合 计 | 100 |
| 4 |
| 5 |
| A、在犯错误的概率不超过0.1%的情况下,有把握说学生对新课程改革工作的满意情况与性别有关 |
| B、在犯错误的概率不超过0.1%的情况下,有把握说学生对新课程改革工作的满意情况与性别无关 |
| C、在犯错误的概率不超过0.5%的情况下,有把握说学生对新课程改革工作的满意情况与性别有关 |
| D、在犯错误的概率不超过0.5%的情况下,有把握说学生对新课程改革工作的满意情况与性别无关 |
在△A BC中,角 A,B,C的对边长分别为a,b,c,a=4,A=45°,B=60°,则b=( )
A、2
| ||
B、2
| ||
C、2
| ||
D、
|