题目内容
1.已知f(x)=$\left\{\begin{array}{l}{-{x}^{2},x≤0}\\{{x}^{3}-3x,x>0}\end{array}\right.$,若直线y=kx-$\frac{1}{4}$与f(x)的图象有三个公共点,则实数k的取值范围是( )| A. | (-$\frac{9}{4}$,+∞) | B. | (0,+∞) | C. | (-$\frac{7}{4}$,+∞) | D. | (-3,-$\frac{9}{4}$)∪(-$\frac{7}{4}$,+∞) |
分析 先画出f(x)的图象,由图象可知,y=kx-$\frac{1}{4}$过定点(-$\frac{1}{4}$,0),当k≥0时,由图象可知,有三个交点,当k<0时,设直线y=kx-$\frac{1}{4}$与f(x)=x3-3x的切点坐标为(x0,y0),利用导数的几何意义求出k的值,再根据斜率公式求出k,继而求出k的值,有图象可知k的范围.
解答 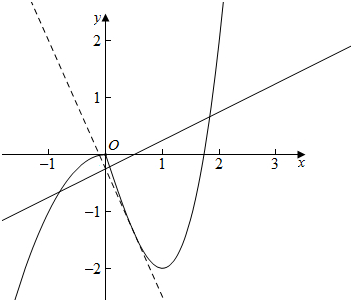 解:画出f(x)=$\left\{\begin{array}{l}{-{x}^{2},x≤0}\\{{x}^{3}-3x,x>0}\end{array}\right.$的图象,如图所示,
解:画出f(x)=$\left\{\begin{array}{l}{-{x}^{2},x≤0}\\{{x}^{3}-3x,x>0}\end{array}\right.$的图象,如图所示,
∵y=kx-$\frac{1}{4}$过定点(-$\frac{1}{4}$,0),
当k≥0时,由图象可知,有三个交点,
当k<0时,
设直线y=kx-$\frac{1}{4}$与f(x)=x3-3x的切点坐标为(x0,y0),
∴f′(x)=3x2-3,
∴f′(x0)=3x02-3=k=$\frac{{y}_{0}+\frac{1}{4}}{{x}_{0}}$,
即3x03-3x0=y0+$\frac{1}{4}$
∵y0=x03-3x0,
∴3x03-3x0=x03-3x0+$\frac{1}{4}$,
解得x0=$\frac{1}{2}$,
∴k=3x02-3=-$\frac{9}{4}$,
∴-$\frac{9}{4}$<k<0时,也有三个交点,
综上所述,k的取值范围为(-$\frac{9}{4}$,+∞).
故选:A.
点评 本题主要考查函数的图象的交点以及数形结合方法,数形结合是数学解题中常用的思想方法,本题由于使用了数形结合的方法,使得问题便迎刃而解,且解法简捷,属于中档题.

练习册系列答案
相关题目
12.将函数$y=2sin(ωx+\frac{π}{3})(ω>0)$的图象分别向左、向右各平移$\frac{π}{3}$个单位后,所得的两个图象的对称轴重合,则ω的最小值为( )
| A. | 3 | B. | $\frac{4}{3}$ | C. | 6 | D. | $\frac{3}{2}$ |
6.在圆C1:x2+y2=4内任取一点P,P落在圆C2:(x-a)2+y2=1内的概率是$\frac{1}{4}$,则a的范围是( )
| A. | -1≤a≤1 | B. | -2≤a≤2 | C. | 0≤a≤1 | D. | -1≤a≤0 |
10.在区间[0,2π]上随机取一个数x,则事件“cosx≥$\frac{1}{2}$”发生的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{11}{12}$ |
 为
为 上的可导函数,且对
上的可导函数,且对 ,均有
,均有 ,则有( )
,则有( )



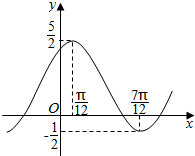 函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,|φ<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,|φ<$\frac{π}{2}$)的图象如图所示.