题目内容
17.设全集U=C,A={z||z-1|=1-|z|,z∈C},B={z||z|<1,z∈C},若z∈A∩(∁UB),求复数z在复平面内对应点的轨迹.分析 由A={z||z-1|=1-|z|,z∈C},得A={z||z-1|+|z|=1,z∈C},进一步求出A的轨迹为线段,由B={z||z|<1,z∈C},即可求出B为以(0,0)为圆心的圆,再由z∈A∩(∁UB)=B,即可求出复数z在复平面内对应点的轨迹.
解答 解:由A={z||z-1|=1-|z|,z∈C},得A={z||z-1|+|z|=1,z∈C},即z到M(1,0)和N(0,0)的距离和为1,
∴A为线段MN.
B={z||z|<1,z∈C},即B在以(0,0)为圆心的圆的内部.
∴∁UB表示复平面内以(0,0)为圆心的圆及其外部的点.
若z∈A∩(∁UB),
则复数z在复平面内对应点的轨迹是点N(1,0).
点评 本题考查了复数的代数表示法及其几何意义,考查了复数z在复平面内对应点的轨迹的求法,是基础题.

练习册系列答案
相关题目
7.已知平面向量$\overrightarrow{a}$=(1,x),$\overrightarrow{b}$=(y,1).若$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数x,y一定满足( )
| A. | xy-1=0 | B. | xy+1=0 | C. | x-y=0 | D. | x+y=0 |
8.已知x>3,则$x+\frac{4}{x-3}$的最小值为( )
| A. | 2 | B. | 4 | C. | 5 | D. | 7 |
2.若曲线y=x2在点(x0,x02)处切线的倾斜角为$\frac{π}{4}$,则x0=( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
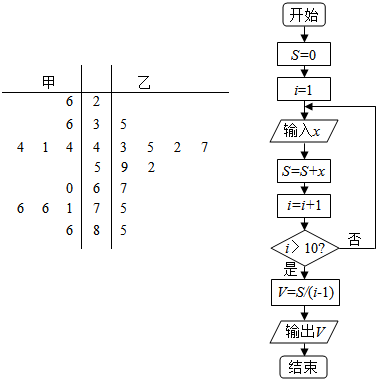 为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.
为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.