题目内容
5.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}(x+1),x>0}\\{-{x}^{2}-3x,x≤0}\end{array}\right.$,若函数g(x)=f(x)-a有3个零点,则实数a的取值范围是(0,$\frac{9}{4}$).分析 将函数g(x)=f(x)-a有3个零点转化为y=f(x)与y=a有三个交点,在同一坐标系中作出两函数的图象,即可求得实数a的取值范围.
解答 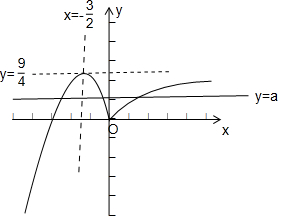 解:∵f(x)=$\left\{\begin{array}{l}{lo{g}_{3}(x+1),x>0}\\{-{x}^{2}-3x,x≤0}\end{array}\right.$,
解:∵f(x)=$\left\{\begin{array}{l}{lo{g}_{3}(x+1),x>0}\\{-{x}^{2}-3x,x≤0}\end{array}\right.$,
∴函数g(x)=f(x)-a有3个零点?
方程f(x)=a有3个根?y=f(x)与y=a有三个交点,
在同一坐标系中作出两函数的图象如下:
由图可知,当0<a<$\frac{9}{4}$时,y=f(x)与y=a有三个交点,即函数g(x)=f(x)-a有3个零点.
故答案为:(0,$\frac{9}{4}$).
点评 本题考查根的存在性及根的个数判断,将函数g(x)=f(x)-a有3个零点转化为y=f(x)与y=a有三个交点是关键,考查等价转化思想与数形结合思想的综合运用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.如果对一切实数x、y,不等式$\frac{y}{4}$-cos2x≥asinx-$\frac{9}{y}$恒成立,则实数a的取值范围是( )
| A. | (-∞,$\frac{4}{3}$] | B. | [3,+∞) | C. | [-2$\sqrt{2}$,2$\sqrt{2}$] | D. | [-3,3] |
10.已知f(x)=a-$\frac{2}{{2}^{x}+1}$(a∈R)是奇函数,那么实数a的值等于( )
| A. | 1 | B. | -1 | C. | 0 | D. | ±1 |
17.以下四个命题中不正确的是 ( )
| A. | $f(x)=\frac{|x|}{x}$是奇函数 | B. | f(x)=x2,x∈(-3,3]是偶函数 | ||
| C. | f(x)=(x-3)2是非奇非偶函数 | D. | y=x4+x2是偶函数 |
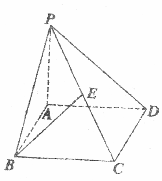 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内,有BE⊥PC于E,且BE=$\frac{{\sqrt{6}}}{3}$a.
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内,有BE⊥PC于E,且BE=$\frac{{\sqrt{6}}}{3}$a.