题目内容
5.设f(x)=|2x-4|+|x+3|.(1)解不等式f(x)>7;
(2)若f(x)-4≥m恒成立,求m的取值范围.
分析 (1)通过讨论x的范围,得到关于x的不等式组,解出即可;(2)先求出f(x)的最小值,得到m+4≤5,从而求出m的范围即可.
解答 解:(1)原不等式可化为:$\left\{\begin{array}{l}{x≥2}\\{3x-1>7}\end{array}\right.$或$\left\{\begin{array}{l}{-3<x<2}\\{7-x>7}\end{array}\right.$或$\left\{\begin{array}{l}{x≤-3}\\{1-3x>7}\end{array}\right.$,
解得x>$\frac{8}{3}$或-3<x<0或x≤-3,
∴原 不等式的解集是(-∞,0)∪($\frac{8}{3}$,+∞);
(2)f(x)=$\left\{\begin{array}{l}{3x-1,x≥2}\\{7-x,-3<x<2}\\{1-3x,x≤-3}\end{array}\right.$,
∴函数f(x)的最小值是5,
∴m+4≤5,解得:m≤1,
即m的范围是(-∞,1].
点评 本题考查了绝对值不等式的解法,考查分类讨论思想,是一道中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
17.在数列{an}中,对任意的n∈N*,都有an-an+1=10,则数列{an}是( )
| A. | 递增数列 | B. | 递减数列 | C. | 常数列 | D. | 摆动数列 |
14.已知集合A={1,2,3},B={x|(x-3)(x-6)=0},则A∩B等于( )
| A. | {1} | B. | {2,3} | C. | {3,6} | D. | {3} |
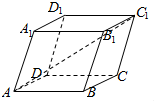 已知平行六面体ABCD-A1B1C1D1所有棱长均为1,∠BAD=∠BAA1=∠DAA1=60°,则AC1的长为$\sqrt{6}$.
已知平行六面体ABCD-A1B1C1D1所有棱长均为1,∠BAD=∠BAA1=∠DAA1=60°,则AC1的长为$\sqrt{6}$.