题目内容
如果双曲线
-
=1(a>0,b>0)的一条渐近线与直线
x-y+
=0平行,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:渐近线与直线3
x-y+
=0平行,得a、b关系,再由双曲线基本量的平方关系,得出a、c的关系式,结合离心率的定义,可得该双曲线的离心率.
| 3 |
| 3 |
解答:
解:∵双曲线
-
=1(a>0,b>0)的一条渐近线与直线
x-y+
=0平行
∴双曲线的渐近线方程为y=±
x
∴
=
,得b2=3a2,c2-a2=3a2,
此时,离心率e=
=2.
故选:C.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
∴双曲线的渐近线方程为y=±
| 3 |
∴
| b |
| a |
| 3 |
此时,离心率e=
| c |
| a |
故选:C.
点评:本题给出双曲线的渐近线方程,求双曲线的离心率,考查了双曲线的标准方程与简单几何性质等知识,属于基础题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
如图程序框图中,若输入m=4,n=10,则输出a,i的值分别是( )


| A、12,4 | B、16,5 |
| C、20,5 | D、24,6 |
已知双曲线
-
=1(a>0,b>0)的一条渐近线与直线x+3y+1=0垂直,则双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列命题中的假命题是( )
| A、?x∈R,lgx=0 |
| B、?x∈R,tanx=2 |
| C、?x∈R,x2≥0 |
| D、?x∈R,2 x2+2x>1 |
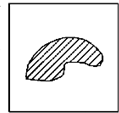 如图,边长为2的正方形有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率为
如图,边长为2的正方形有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率为| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
| D、无法计算 |
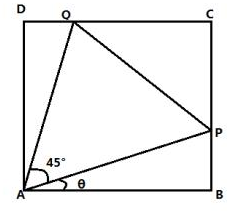 如图的正方形ABCD边长为1,P,Q为线段BC,CD上的动点,设∠PAB=θ,且tanθ=t,∠PAQ=45°.
如图的正方形ABCD边长为1,P,Q为线段BC,CD上的动点,设∠PAB=θ,且tanθ=t,∠PAQ=45°.