题目内容
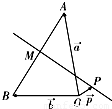
如图,已知⊙O是△ABC的外接圆,AB为直径,若PA⊥AB,PO过AC的中点M,求证:PC是⊙O的切线.
【答案】分析:要证PC是⊙O的切线,只要连接OC,再证∠PCO=90°即可.由△PAO≌△PCO,可证得∠PCO=90°.
解答: 证明:连接OC,
证明:连接OC,
∵PA⊥AB,
∴∠PA0=90°.(1分)
∵PO过AC的中点M,OA=OC,
∴PO平分∠AOC.
∴∠AOP=∠COP.(3分)
∴在△PAO与△PCO中有OA=OC,∠AOP=∠COP,PO=PO.
∴△PAO≌△PCO.(6分)
∴∠PCO=∠PA0=90°.
即PC是⊙O的切线.(7分)
点评:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.
解答:
 证明:连接OC,
证明:连接OC,∵PA⊥AB,
∴∠PA0=90°.(1分)
∵PO过AC的中点M,OA=OC,
∴PO平分∠AOC.
∴∠AOP=∠COP.(3分)
∴在△PAO与△PCO中有OA=OC,∠AOP=∠COP,PO=PO.
∴△PAO≌△PCO.(6分)
∴∠PCO=∠PA0=90°.
即PC是⊙O的切线.(7分)
点评:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
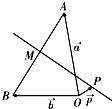 如图,已知O、A、B是平面上三点,向量
如图,已知O、A、B是平面上三点,向量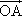 =a,
=a,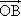 =b,
=b,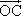 =c,且|a|=2,|b|=1,|c|=3,试用a和b表示c.
=c,且|a|=2,|b|=1,|c|=3,试用a和b表示c.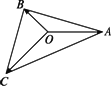
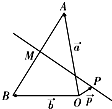 如图,已知O、A、B是平面上三点,向量
如图,已知O、A、B是平面上三点,向量 =
= ,
, =
= .在平面AOB上,P是线段AB垂直平分线上任意一点,向量
.在平面AOB上,P是线段AB垂直平分线上任意一点,向量 =
= ,且|
,且| )的值是
)的值是



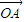 =
=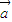 ,
,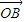 =
=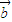 .在平面AOB上,P是线段AB垂直平分线上任意一点,向量
.在平面AOB上,P是线段AB垂直平分线上任意一点,向量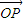 =
=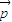 ,且|
,且|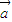 |=3,|
|=3,|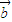 |=2,则
|=2,则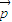 •(
•(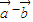 )的值是( )
)的值是( )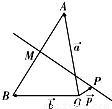




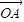 =
=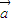 ,
,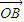 =
=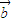 .在平面AOB上,P是线段AB垂直平分线上任意一点,向量
.在平面AOB上,P是线段AB垂直平分线上任意一点,向量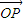 =
=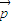 ,且|
,且|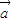 |=3,|
|=3,|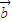 |=2,则
|=2,则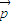 •(
•(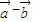 )的值是( )
)的值是( )