题目内容
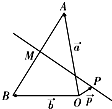 如图,已知O、A、B是平面上三点,向量
如图,已知O、A、B是平面上三点,向量 =
= ,
, =
= .在平面AOB上,P是线段AB垂直平分线上任意一点,向量
.在平面AOB上,P是线段AB垂直平分线上任意一点,向量 =
= ,且|
,且| |=3,|
|=3,| |=2,则
|=2,则 •(
•( )的值是
)的值是
- A.

- B.

- C.

- D.

D
分析:因为 =
= 与向量
与向量 垂直,得
垂直,得 •(
•( )=
)= •
• =0,因此将向量
=0,因此将向量 表示成
表示成 的和,从而
的和,从而 •(
•( )=
)= =
= (
( -
- ),代入题中的数据即可得到
),代入题中的数据即可得到 •(
•( )的值.
)的值.
解答: 解:连接OM,根据题意得
解:连接OM,根据题意得 =
=
∵ =
= =
=
∴ •(
•( )=(
)=( )•(
)•( )=
)= (
( )+
)+ •(
•( )
)
∵ =
= ,
, ⊥
⊥ ,得
,得 •(
•( )=
)= •
• =0
=0
∴ •(
•( )=
)= (
( )=
)= (
( -
- )=
)= (32-22)=
(32-22)=
故选:D
点评:本题给出三角形的边AB的垂直平分线,求向量的数量积,着重考查了线段垂直平分线的性质、向量的线性运算和数量积运算性质等知识,属于基础题.
分析:因为
 =
= 与向量
与向量 垂直,得
垂直,得 •(
•( )=
)= •
• =0,因此将向量
=0,因此将向量 表示成
表示成 的和,从而
的和,从而 •(
•( )=
)= =
= (
( -
- ),代入题中的数据即可得到
),代入题中的数据即可得到 •(
•( )的值.
)的值.解答:
 解:连接OM,根据题意得
解:连接OM,根据题意得 =
=
∵
 =
= =
=
∴
 •(
•( )=(
)=( )•(
)•( )=
)= (
( )+
)+ •(
•( )
)∵
 =
= ,
, ⊥
⊥ ,得
,得 •(
•( )=
)= •
• =0
=0∴
 •(
•( )=
)= (
( )=
)= (
( -
- )=
)= (32-22)=
(32-22)=
故选:D
点评:本题给出三角形的边AB的垂直平分线,求向量的数量积,着重考查了线段垂直平分线的性质、向量的线性运算和数量积运算性质等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
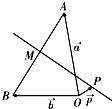 如图,已知O、A、B是平面上三点,向量
如图,已知O、A、B是平面上三点,向量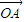 =
=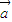 ,
,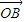 =
=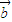 .在平面AOB上,P是线段AB垂直平分线上任意一点,向量
.在平面AOB上,P是线段AB垂直平分线上任意一点,向量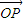 =
=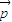 ,且|
,且|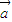 |=3,|
|=3,|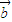 |=2,则
|=2,则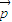 •(
•(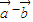 )的值是( )
)的值是( )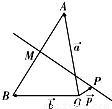




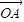 =
=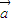 ,
,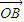 =
=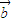 .在平面AOB上,P是线段AB垂直平分线上任意一点,向量
.在平面AOB上,P是线段AB垂直平分线上任意一点,向量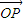 =
=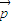 ,且|
,且|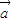 |=3,|
|=3,|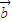 |=2,则
|=2,则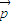 •(
•(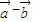 )的值是( )
)的值是( )




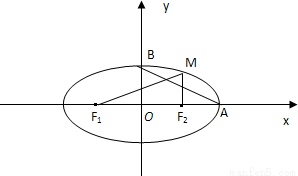
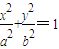 (a>b>0),M为椭圆上的一个动点,F1、F2分别为椭圆的左、右焦点,A、B分别为椭圆的一个长轴端点与短轴的端点.当MF2⊥F1F2时,原点O到直线MF1的距离为
(a>b>0),M为椭圆上的一个动点,F1、F2分别为椭圆的左、右焦点,A、B分别为椭圆的一个长轴端点与短轴的端点.当MF2⊥F1F2时,原点O到直线MF1的距离为 |OF1|.
|OF1|.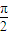 ;
;