题目内容
已知函数f﹙x﹚=a-
,a∈R,若a=1,当x∈[1,+∞﹚时,有tf﹙x﹚≤2x-2恒成立,求实数t的取值范围.
| 2 |
| 2x+1 |
考点:函数恒成立问题
专题:函数的性质及应用
分析:先将a=1时的原函数进行化简,代入不等式,结合已知的x范围,可以判定f(x)>0恒成立,再将t分离出来,此时只需t小于或等于右边函数式的最小值即可,求该函数的最小值时,将2x-1换元成t可能更好.
解答:
解:将a=1代入函数f﹙x﹚=a-
,得f(x)=1-
,因为x≥1,所以2x+1≥3,则
∈(0,1),所以f(x)>0,
所以要使x∈[1,+∞﹚时,有tf﹙x﹚≤2x-2恒成立,
只需t≤
(x≥1)恒成立即可,将f(x)代入化简后得t≤
,令m=2x-1∈[1,+∞),
则问题转化为t≤m-
+1,m∈[1,+∞)时恒成立,又因为t=m-
+1在[1,+∞)上是增函数,
所以t≤(m-
+1)min=(1-2+1)=0,符合题意.
故t的范围是(-∞,0].
| 2 |
| 2x+1 |
| 2 |
| 2x+1 |
| 2 |
| 2x+1 |
所以要使x∈[1,+∞﹚时,有tf﹙x﹚≤2x-2恒成立,
只需t≤
| 2x-2 |
| f(x) |
| (2x+1)(2x-2) |
| 2x-1 |
则问题转化为t≤m-
| 2 |
| m |
| 2 |
| m |
所以t≤(m-
| 2 |
| m |
故t的范围是(-∞,0].
点评:本题考查了不等式恒成立问题,先分离参数(能分离尽量分离),然后转化为求函数的最值问题,要注意中间用换元法时中间量的范围.

练习册系列答案
相关题目
以下程序的功能是( )


| A、计算3×10的值 |
| B、计算355的值 |
| C、计算310的值 |
| D、计算1×2×3×…×10的值 |
某班班会准备从含甲、乙的7人中选取4人发言,要求甲、乙两人至少有一人参加,且若甲、乙同时参加,则他们发言时顺序不能相邻,那么不同的发言顺序有( )
| A、720种 | B、520种 |
| C、600种 | D、360种 |
对于三段论“因为指数函数y=ax是增函数,y=(
)x是指数函数,所以y=(
)x是增函数”,下列说法正确的是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、是一个正确的推理 |
| B、大前提错误导致结论错误 |
| C、小前提错误导致结论错误 |
| D、推理形式错误导致结论错误 |
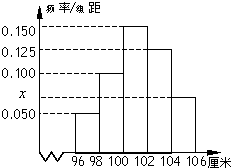 某幼儿园根据部分同年龄段女童的身高数据绘制了频率分布直方图,其中身高的变化范围是[96,106](单位:厘米),样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].
某幼儿园根据部分同年龄段女童的身高数据绘制了频率分布直方图,其中身高的变化范围是[96,106](单位:厘米),样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].