题目内容
9.m,n是空间两条不同直线,α,β是两个不同平面.有以下四个命题:①若m∥α,n∥β且α∥β,则m∥n;
②若m⊥α,n⊥β且α⊥β,则m⊥n;
③若m⊥α,n∥β且α∥β,则m⊥n;
④若m∥α,n⊥β且α⊥β,则m∥n.
其中真命题的序号是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
分析 ①m∥n或m,n相交或m,n异面;②由面面垂直和线面垂直的性质得m⊥n;③判断m⊥β,即可得出结论;④若m∥α,n⊥β且α⊥β,则m∥n或m,n相交或m,n异面.
解答 解:①若m∥α,n∥β,α∥β,则m∥n或m,n相交或m,n异面,故①错误
②若m⊥α,n⊥β,且α⊥β,则由面面垂直和线面垂直的性质得m⊥n,故正确.
③若m⊥α,且α∥β,则m⊥β,∵n∥β,∴m⊥n,故正确;
④若m∥α,n⊥β且α⊥β,则m∥n或m,n相交或m,n异面,故错误.
故选:B.
点评 本题主要题考查的知识点是平面的基本性质及推论,空间直线与平面位置关系的判断,其中根据面面平行,线面垂直的判定及性质,空间直线与平面位置关系的定义和几何特征.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
17.程序框图如图所示,当$A=\frac{12}{13}$时,输出的k的值为( )


| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
4.“x-1>0”是“x2-1>0”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.在复平面内,复数z=i(1+i),那么|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
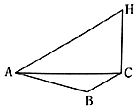 为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气候仪器,这种仪器可以弹射到空中进行气候观测,如图所示,A,B,C三地位于同一水平面上,这种仪器在C地进行弹射实验,观测点A,B两地相距100米,∠BAC=60°,在A地听到弹射声音比B地晚$\frac{2}{17}$秒(已知声音传播速度为340米/秒),在A地测得该仪器至高点H处的仰角为30°,则这种仪器的垂直弹射高度HC=140$\sqrt{3}$米.
为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气候仪器,这种仪器可以弹射到空中进行气候观测,如图所示,A,B,C三地位于同一水平面上,这种仪器在C地进行弹射实验,观测点A,B两地相距100米,∠BAC=60°,在A地听到弹射声音比B地晚$\frac{2}{17}$秒(已知声音传播速度为340米/秒),在A地测得该仪器至高点H处的仰角为30°,则这种仪器的垂直弹射高度HC=140$\sqrt{3}$米.