题目内容
已知数列{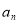 }中,
}中,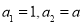 ,且
,且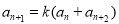 对任意正整数都成立,数列{
对任意正整数都成立,数列{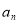 }的前n项和为Sn。
}的前n项和为Sn。
(1)若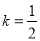 ,且
,且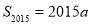 ,求a;
,求a;
(2)是否存在实数k,使数列{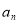 }是公比不为1的等比数列,且任意相邻三项
}是公比不为1的等比数列,且任意相邻三项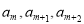 按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
(3)若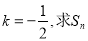 。
。
(1) (2)
(2) (3)
(3)


【解析】
试题分析:(1) 时,
时, ,由等差数列定义知数列
,由等差数列定义知数列 是等差数列,由
是等差数列,由 可得
可得 ,解得
,解得 ,(2)等差数列与等比数列的综合,从等差数列列等量关系:因为数列{
,(2)等差数列与等比数列的综合,从等差数列列等量关系:因为数列{ }是公比不为1,所以
}是公比不为1,所以 不为等差中项,只需讨论
不为等差中项,只需讨论 与
与 为等差中项:若
为等差中项:若 为等差中项,则
为等差中项,则 ,即
,即 ,化简得:
,化简得: ,解得
,解得 (舍1);
(舍1); ;同理若
;同理若 为等差中项,
为等差中项, (3)
(3) 则
则 ,
, ,从而
,从而 ,所以求和时要重新组合,每两项作为一组,先求
,所以求和时要重新组合,每两项作为一组,先求 是偶数时,
是偶数时,

 ,再求
,再求 是奇数时,
是奇数时,



 ,
,
试题解析:(1) 时,
时, ,
, ,所以数列
,所以数列 是等差数列 1分
是等差数列 1分
此时首项 ,公差
,公差 ,数列
,数列 的前
的前 项和是
项和是 3分
3分
故 ,即
,即 ,得
,得 ; 4分
; 4分
(没有过程,直接写 不给分)
不给分)
(2)设数列 是等比数列,则它的公比
是等比数列,则它的公比 ,所以
,所以 ,
, ,
, 6分
6分
①若 为等差中项,则
为等差中项,则 ,即
,即 ,解得:
,解得: ,不合题意;
,不合题意;
②若 为等差中项,则
为等差中项,则 ,即
,即 ,化简得:
,化简得: ,
,
解得 (舍1);
(舍1); ;
;
③若 为等差中项,则
为等差中项,则 ,即
,即 ,化简得:
,化简得: ,
,
解得 ;
; ; 9分
; 9分
综上可得,满足要求的实数 有且仅有一个,
有且仅有一个, ; 10分
; 10分
(3) 则
则 ,
,
 ,
, , 12分
, 12分
当 是偶数时,
是偶数时,


 ,
,
当 是奇数时,
是奇数时,




 ,
, 也适合上式, 15分
也适合上式, 15分
综上可得,

 . 16分
. 16分
考点:等差数列与等比数列
考点分析: 考点1:等比数列 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的定义域是
的定义域是 ;
; 的图象经过点
的图象经过点 则该函数为偶函数;
则该函数为偶函数; 的值域是
的值域是
 ,则
,则 的值是 .
的值是 .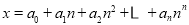 ,其中
,其中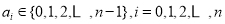 ,且
,且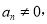 记满足条件的所有x的和为
记满足条件的所有x的和为 ,
,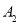 (2)设
(2)设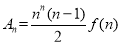 ,求
,求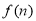
 的最小值为2,则a=
的最小值为2,则a=
 ,则
,则 的最小值为
的最小值为
 的右焦点到渐近线的距离是其到左顶点距离的一半,则双曲线的
的右焦点到渐近线的距离是其到左顶点距离的一半,则双曲线的 .
. ,且
,且 共线,其中
共线,其中 .
. 的值;
的值; ,求
,求 的值.
的值.