题目内容
对于给定的大于1的正整数n,设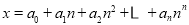 ,其中
,其中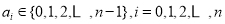 ,且
,且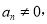 记满足条件的所有x的和为
记满足条件的所有x的和为 ,
,
(1)求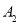 (2)设
(2)设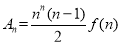 ,求
,求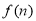
(1)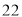 .(2)
.(2)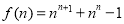
【解析】
试题分析:(1)实质为读题:当 时,
时, ,
,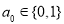 ,
,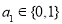 ,
,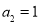 ,所以
,所以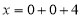 ,
,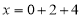 ,
,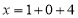 ,
,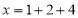 ,
,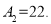
(2)问题实质为统计出现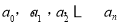 的次数,
的次数,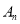 中所有含
中所有含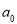 项的和为
项的和为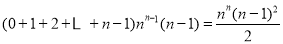 ;同理,
;同理,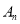 中所有含
中所有含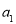 项的和为
项的和为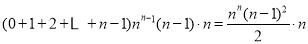 ;
;
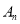 中所有含
中所有含 项的和为
项的和为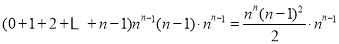 ;而
;而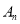 中所有含
中所有含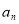 项的和为
项的和为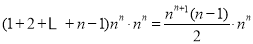 ;
;
所以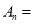
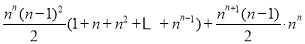 ;
;
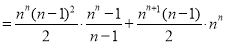
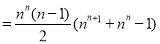 ,
,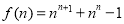
试题解析:(1)当 时,
时, ,
,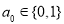 ,
,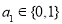 ,
,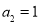 ,
,
故满足条件的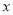 共有
共有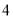 个,
个,
分别为: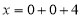 ,
,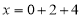 ,
,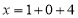 ,
,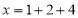 ,
,
它们的和是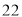 . 4分
. 4分
(2)由题意得,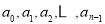 各有
各有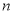 种取法;
种取法;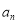 有
有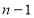 种取法,
种取法,
由分步计数原理可得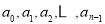 的不同取法共有
的不同取法共有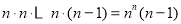 ,
,
即满足条件的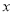 共有
共有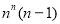 个, 6分
个, 6分
当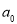 分别取
分别取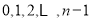 时,
时,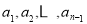 各有
各有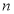 种取法,
种取法,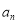 有
有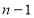 种取法,
种取法,
故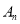 中所有含
中所有含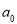 项的和为
项的和为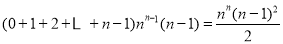 ;
;
同理,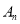 中所有含
中所有含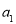 项的和为
项的和为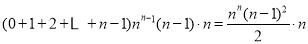 ;
;
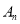 中所有含
中所有含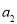 项的和为
项的和为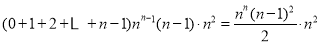 ;
;
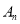 中所有含
中所有含 项的和为
项的和为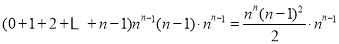 ;
;
当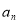 分别取
分别取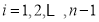 时,
时,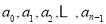 各有
各有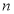 种取法,
种取法,
故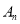 中所有含
中所有含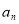 项的和为
项的和为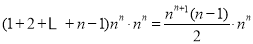 ;
;
所以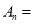
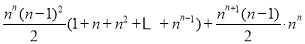 ;
;
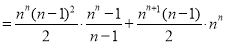
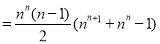
故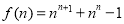 . 10分
. 10分
考点:分布计算原理
考点分析: 考点1:等比数列 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 ,且α是第二象限的角,求tan(
,且α是第二象限的角,求tan(  +α) 的值.
+α) 的值. ,则
,则 的值域是 ( )
的值域是 ( ) B.
B.  C.
C. D.
D. 
 ,则二面角
,则二面角 的余弦值为 【 】
的余弦值为 【 】 B、
B、 C、
C、  D、
D、
 如下:
如下: ,且当
,且当 时,
时, ,其中
,其中 是不同的质数.
是不同的质数. 为12的全部不同正因数的集合,则
为12的全部不同正因数的集合,则 .
.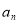 }中,
}中,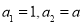 ,且
,且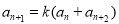 对任意正整数都成立,数列{
对任意正整数都成立,数列{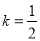 ,且
,且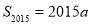 ,求a;
,求a;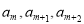 按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;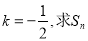 。
。
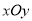 中,角
中,角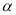 的终边经过点
的终边经过点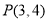 .
.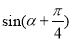 的值;
的值;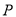 关于
关于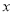 轴的对称点为
轴的对称点为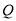 ,求
,求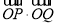 的值.
的值.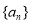 中
中
 .
.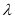 ,使数列
,使数列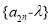 是等比数列?若存在,求
是等比数列?若存在,求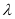 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;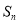 是数列
是数列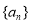 的前
的前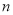 项和,求满足
项和,求满足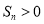 的所有正整数
的所有正整数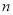 .
.