题目内容
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=
AE=2,O、M分别为CE、AB的中点.
(1)求异面直线AB与CE所成角的大小.
(2)求直线CD和平面ODM所成角的正弦值.
| 1 |
| 2 |
(1)求异面直线AB与CE所成角的大小.
(2)求直线CD和平面ODM所成角的正弦值.


(1)∵DB⊥BA,又∵面ABDE⊥面ABC,面ABDE∩面ABC=AB,DB?面ABDE,
∴DB⊥面ABC,∵BD∥AE,∴EA⊥面ABC,
如图所示,以C为原点,分别以CA,CB为x,y轴,
以过点C且与平面ABC垂直的直线为z轴,建立空间直角坐标系,
∵AC=BC=4,
∴设各点坐标为C(0,0,0),A(4,0,0),B(0,4,0),D(0,4,2),E(4,0,4),
则O(2,0,2),M(2,2,0),
| CD |
| OD |
| MD |
| AB |
| CE |
∴cos<
| AB |
| CE |
| -16 | ||||
4
|
| 1 |
| 2 |
∴异面直线AB与CE所成角的大小为60°.
(2)设平面ODM的法向量
| n |
| n |
| OD |
且
| n |
| MD |
|
令x=2,则y=1,z=1,∴
| n |
设直线CD和平面ODM所成角为θ,
则sinθ=|cos<
| n |
| CD |
| 0+4+2 | ||||
|
| 6 | ||
2
|
| ||
| 10 |
∴直线CD和平面ODM所成角的正弦值为
| ||
| 10 |

练习册系列答案
相关题目
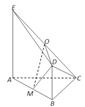 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,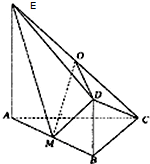 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA, 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,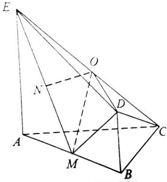 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形, 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=