题目内容
 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=| 1 | 2 |
(1)求证:OD∥平面ABC;
(2)在棱EM上是否存在N,使ON⊥平面ABDE?若能,请指出点N的位置,并加以证明;若不能,请说明理由;
(3)求二面角O-ED-M的大小.
分析:(1)取AC中点F,连OF、BF,通过证明四边形ODBF为平行四边形,得出OD∥FB,从而证出OD∥平面ABC
(2)存在.当N是EM中点时即可.先由CM⊥AB,结合面面垂直的性质定理得出BC⊥平面EDM,再由ON是△EMC的中位线,得出ON∥CM,所以有ON⊥平面ABDE.
(3)法1:过N作NG⊥ED于点G,连接OG、ON,可以证明∠OGN即所求二面角的平面角.在△OGN求解即可.
法2:如图建立直角坐标系.分别求出面OED 的法向量,平面MED的法向量,利用向量的夹角求出二面角O-ED-M的大小.
(2)存在.当N是EM中点时即可.先由CM⊥AB,结合面面垂直的性质定理得出BC⊥平面EDM,再由ON是△EMC的中位线,得出ON∥CM,所以有ON⊥平面ABDE.
(3)法1:过N作NG⊥ED于点G,连接OG、ON,可以证明∠OGN即所求二面角的平面角.在△OGN求解即可.
法2:如图建立直角坐标系.分别求出面OED 的法向量,平面MED的法向量,利用向量的夹角求出二面角O-ED-M的大小.
解答:解:(1)取AC中点F,连OF、BF,
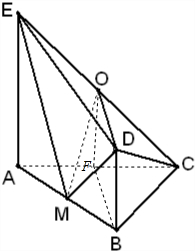
由于O为CE的中点,∴OF是△CAE的中位线,∴OF∥AE,OF=
AE,
又BD∥AE,BD=
AE=2,∴OF∥BD,OF=BD,
∴四边形ODBF为平行四边形,
∴OD∥FB,又OD?平面ABC,FB?平面ABC,
∴OD∥平面ABC;
(2)存在.当N是EM中点时即可.
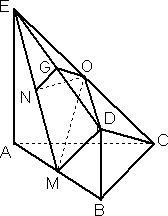
由已知,ON是△EMC的中位线,∴ON∥CM
∵△ABC是等腰直角三角形,
∴CM⊥AB,
又平面ABDE⊥平面ABC,根据面面垂直的性质定理得出
CM⊥平面EDM,而ON与CM平行,从而可得ON⊥平面EDM.
(3)法1:过N作NG⊥ED于点G,连接OG、ON,
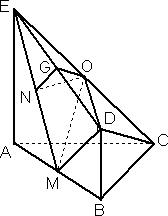
由(2)ON⊥平面EDM,ED?平面EDM,
∴ON⊥ED,ON∩NG=N,
∴ED⊥ONG,ED⊥OG,
则∠OGN即所求二面角的平面角.
在Rt△ONG中,由题计算可知ON=
,OG=2,
又∠ONG是直角,所以∠OGN=
,故二面角O-ED-M的大小是
.
法2:如图建立直角坐标系.
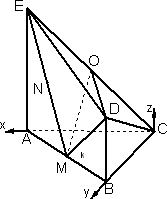
可知D(0,4,2),E(4,0,4),O(2,0,2),M(2,2,0),由(2)知N(3,1,2),所以平面EMD的法向量
=(-1,-1,0),
设平面OED的法向量为
=(x,y,1),
又知
=(2,0,2),
=(-2,4,0),由
•
=0
及
•
=0得
计算可得
所以
=(-1,-
,1),cos<
,
>=
,二面角O-ED-M的大小是
.

由于O为CE的中点,∴OF是△CAE的中位线,∴OF∥AE,OF=
| 1 |
| 2 |
又BD∥AE,BD=
| 1 |
| 2 |
∴四边形ODBF为平行四边形,
∴OD∥FB,又OD?平面ABC,FB?平面ABC,
∴OD∥平面ABC;
(2)存在.当N是EM中点时即可.

由已知,ON是△EMC的中位线,∴ON∥CM
∵△ABC是等腰直角三角形,
∴CM⊥AB,
又平面ABDE⊥平面ABC,根据面面垂直的性质定理得出
CM⊥平面EDM,而ON与CM平行,从而可得ON⊥平面EDM.
(3)法1:过N作NG⊥ED于点G,连接OG、ON,

由(2)ON⊥平面EDM,ED?平面EDM,
∴ON⊥ED,ON∩NG=N,
∴ED⊥ONG,ED⊥OG,
则∠OGN即所求二面角的平面角.
在Rt△ONG中,由题计算可知ON=
| 2 |
又∠ONG是直角,所以∠OGN=
| π |
| 4 |
| π |
| 4 |
法2:如图建立直角坐标系.

可知D(0,4,2),E(4,0,4),O(2,0,2),M(2,2,0),由(2)知N(3,1,2),所以平面EMD的法向量
| NO |
设平面OED的法向量为
| n |
又知
| OE |
| OD |
| n |
| OE |
及
| n |
| OD |
|
|
所以
| n |
| 1 |
| 2 |
| n |
| NO |
| ||
| 2 |
| π |
| 4 |
点评:本题考查空间直线和平面平行,直线和平面垂直的判定,二面角大小求解.考查空间想象、推理论证能力.利用空间向量的方法,能降低思维难度,思路相对固定,是人们研究解决几何体问题又一有力工具.

练习册系列答案
相关题目
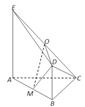 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,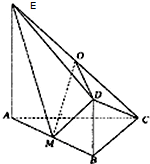 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA, 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,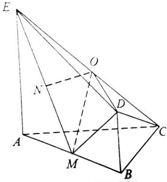 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,