题目内容
15.向边长为a的正三角形内任投一点,点落在三角形内切圆内的概率是$\frac{\sqrt{3}π}{9}$.分析 求出正三角形的面积与其内切圆的面积,即可求出对应的概率.
解答 解:∵正三角形边长为a,
∴该正三角形的面积S正三角形=$\frac{\sqrt{3}}{4}$a2
其内切圆半径为r=$\frac{1}{3}$×$\frac{\sqrt{3}}{2}$a=$\frac{\sqrt{3}}{6}$a,
内切圆面积为S内切圆=πr2=$\frac{π}{12}$a2;
∴点落在圆内的概率为
P=$\frac{{S}_{内切圆}}{{S}_{正三角形}}$=$\frac{{\frac{π}{12}a}^{2}}{{\frac{\sqrt{3}}{4}a}^{2}}$=$\frac{\sqrt{3}π}{9}$.
故答案为:$\frac{\sqrt{3}π}{9}$.
点评 本题考查了几何概型的计算问题,解题的关键是弄清几何测度思维什么,属于基础题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
6.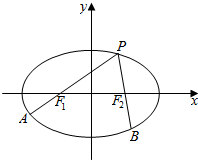 如图,F1F2为椭圆C:$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1的左、右焦点,点P为椭圆C上一点,延长PF1、,PF2分别交椭圆C于A,B.若$\overrightarrow{P{F}_{1}}$=2$\overrightarrow{{F}_{1}A}$,$\overrightarrow{P{F}_{2}}$=$λ\overrightarrow{{F}_{2}B}$,则λ=( )
如图,F1F2为椭圆C:$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1的左、右焦点,点P为椭圆C上一点,延长PF1、,PF2分别交椭圆C于A,B.若$\overrightarrow{P{F}_{1}}$=2$\overrightarrow{{F}_{1}A}$,$\overrightarrow{P{F}_{2}}$=$λ\overrightarrow{{F}_{2}B}$,则λ=( )
 如图,F1F2为椭圆C:$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1的左、右焦点,点P为椭圆C上一点,延长PF1、,PF2分别交椭圆C于A,B.若$\overrightarrow{P{F}_{1}}$=2$\overrightarrow{{F}_{1}A}$,$\overrightarrow{P{F}_{2}}$=$λ\overrightarrow{{F}_{2}B}$,则λ=( )
如图,F1F2为椭圆C:$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1的左、右焦点,点P为椭圆C上一点,延长PF1、,PF2分别交椭圆C于A,B.若$\overrightarrow{P{F}_{1}}$=2$\overrightarrow{{F}_{1}A}$,$\overrightarrow{P{F}_{2}}$=$λ\overrightarrow{{F}_{2}B}$,则λ=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
3.如图,直线l经过第二、第三、第四象限,l的倾斜角为α,斜率为k,则( )


| A. | ksin(π+α)>0 | B. | kcos(π-α)>0 | C. | ksinα≤0 | D. | kcosα≤0 |
9.若集合U={1,2,3,4,5},A={1,2,3},B={2,3,4},则∁U(A∪B)=( )
| A. | {5} | B. | {2} | C. | {1,2,3,4} | D. | {1,3,4,5} |
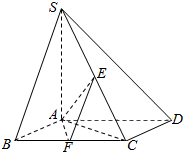 如图,已知四棱锥S-ABCD,底面ABCD为菱形,SA⊥平面ABCD,∠ADC=60°,E,F分别是SC,BC的中点.
如图,已知四棱锥S-ABCD,底面ABCD为菱形,SA⊥平面ABCD,∠ADC=60°,E,F分别是SC,BC的中点.