题目内容
10．已知函数f（x）在[-2，2]上是奇函数，在区间[0，2]上是减函数，且f（a-1）＜f（2-a），则a的取值范围是$\frac{3}{2}$＜a≤3．分析 利用函数f（x）在[-2，2]上是奇函数，在区间[0，2]上是减函数，可得y=f（x）在定义域[-2，2]上是减函数，将不等式f（a-1）＜f（2-a），转化为-2≤2-a＜a-1≤2进行求解．
解答 解：∵函数f（x）在[-2，2]上是奇函数，在区间[0，2]上是减函数，
∴y=f（x）在定义域[-2，2]上是减函数
∵f（a-1）＜f（2-a），
∴有-2≤2-a＜a-1≤2，解得$\frac{3}{2}$＜a≤3．
故答案为：$\frac{3}{2}$＜a≤3．
点评 本题主要考查函数奇偶性和单调性的应用，利用函数的奇偶性将不等式进行转化是解决本题的关键，综合考查函数的性质．
练习册系列答案
相关题目
20．抛物线C：y2=4x上一点P到焦点F的距离为5，则点P的坐标为（ ）
| A． | （1，2） | B． | （2，2$\sqrt{2}$） | C． | （3，2$\sqrt{3}$） | D． | （4，±4） |
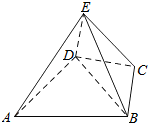如图，几何体E-ABCD是四棱锥，△ABD为正三角形，CB=CD，EC⊥BD．
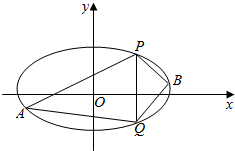已知椭圆C的中心在坐标原点，离心率为$\frac{1}{2}$，且它的短轴端点恰好是双曲线$\frac{y^2}{8}-\frac{x^2}{4}=1$的焦点．