题目内容
已知函数f(x)=xln x.
(1)若函数g(x)=f(x)+x2+ax+2有零点,求实数a的最大值;
(2)若∀x>0,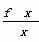 ≤x-kx2-1恒成立,求实数k的取值范围.
≤x-kx2-1恒成立,求实数k的取值范围.
(1)由题知,g(x)=xln x+x2+ax+2=0在(0,+∞)上有实根,
即:-a=ln x+x+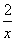 在(0,+∞)上有实根,
在(0,+∞)上有实根,
令φ(x)=ln x+x+ ,则φ′(x)=
,则φ′(x)= +1-
+1-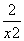 =
=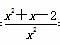 =
=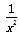 (x+2)(x-1),
(x+2)(x-1),
易知,φ(x)在(0,1)上单调递减,在(1,+∞)上单调递增,所以,-a≥φ(x)max=φ(1)=3,a≤-3.
(2)依题意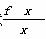 ≤x-kx2-1,kx2≤x-1-ln x,x>0.
≤x-kx2-1,kx2≤x-1-ln x,x>0.
所以k≤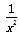 (x-1-ln x)
(x-1-ln x)
设g(x)=x-1-ln x,x>0,g′(x)=1- ,
,
当0<x<1时g′(x)<0,
当x>1时g′(x)>0,所以∀x>0,g(x)≥g(1)=0.
所以,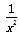 (x-1-ln x)≥0,
(x-1-ln x)≥0,
∴k≤0,即k的取值范围是(-∞,0].

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 ,求A∪B.
,求A∪B. ,若函数f(x)是奇函数,则g(-4)=________.
,若函数f(x)是奇函数,则g(-4)=________. 的定义域为________.
的定义域为________.