题目内容
1.若定义在(-1,1)上的函数f(x)满足:对任意x,y∈(-1,1),都有$f(x)+f(y)=f(\frac{x+y}{1+xy})$,则称f(x)为漂亮函数.(1)已知$g(x)=lg\frac{1-x}{1+x}$,问g(x)是否为漂亮函数,并说明理由;
(2)已知f(x)为漂亮函数,判断f(x)的奇偶性;
(3)若漂亮函数f(x)满足:当x∈(0,1)时,都有f(x)>0,试判断f(x)在(-1,1)上的单调性,并给出证明.
分析 (1)根据平了函数的定义,证明g(x)+g(y)=g($\frac{x+y}{1+xy}$),即可.
(2)利用赋值法,x=y=0求出f(0)的值,结合y=-x,利用已知条件,推出函数是奇函数即可.
(3)先设0<x1<x2<1,然后作差求f(x1)-f(x2),根据题目条件进行化简变形判定其符号,根据函数单调性的定义即可判定.
解答 解:(1)∵g(x)+g(y)=lg$\frac{1-x}{1+x}$+lg$\frac{1-y}{1+y}$=lg($\frac{1-x}{1+x}$•$\frac{1-y}{1+y}$)=lg$\frac{1+xy-(x+y)}{1+xy+x+y}$,
g($\frac{x+y}{1+xy}$)=lg$\frac{1-\frac{x+y}{1+xy}}{1+\frac{x+y}{1+xy}}$=lg$\frac{1+xy-(x+y)}{1+xy+x+y}$,
则g(x)+g(y)=g($\frac{x+y}{1+xy}$),成立,即g(x)是漂亮函数.
证明:由x=y=0得f(0)+f(0)=f($\frac{0+0}{1+0}$)=f(0),∴f(0)=0,
任取x∈(-1,1),则-x∈(-1,1),f(x)+f(-x)=f($\frac{x-x}{1-{x}^{2}}$)=f(0)=0.
∴f(x)+f(-x)=0,
即f(x)=-f(-x).
∴f(x)在(-1,1)上为奇函数.
f(x)在(-1,1)上单调递增,
∵f(x)在(-1,1)上为奇函数,且f(0)=0,
∴只需要证明当x∈(0,1)时,函数的单调性即可,
证明:设0<x1<x2<1,则f(x1)-f(x2)=f(x1)+f(-x2)=f($\frac{{x}_{1}{-x}_{2}}{1-{x}_{1}{x}_{2}}$).
∵x∈(0,1)时,都有f(x)>0,
∴x∈(-1,0)时,都有f(x)<0
而x1-x2<0,0<x1x2<1所以-1<$\frac{{x}_{1}{-x}_{2}}{1-{x}_{1}{x}_{2}}$<0
∵当x∈(-1,0)时,f(x)<0
∴f(x1)-f(x2)=f(x1)+f(-x2)=f($\frac{{x}_{1}{-x}_{2}}{1-{x}_{1}{x}_{2}}$)<0
即当x1<x2时,f(x1)<f(x2).
∴f(x)在(0,1)上单调递增.
即f(x)在(-1,1)上单调递增
点评 本题主要考查抽象函数的应用以及,函数的单调性的判定与证明,以及函数奇偶性的判定,函数的奇偶性是函数在定义域上的“整体”性质,单调性是函数的“局部”性质,综合考查函数的性质.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{2}$+1 | D. | $\sqrt{5}$ |
| A. | 1990 | B. | 1991 | C. | 1989 | D. | 1988 |
| A. | {x|0≤x≤1} | B. | {x|x≥0} | C. | {x|x≥1,或x<0} | D. | {x|0<x≤1} |
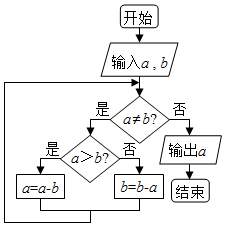 如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若在框图中输入的a,b分别为30、18,则输出的a为( )
如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若在框图中输入的a,b分别为30、18,则输出的a为( )