题目内容
1.复数z=$\frac{2}{1-i}$(i为虚数单位),则( )| A. | z的实部为2 | B. | z的虚部为i | C. | $\overline z$=1+i | D. | |z|=$\sqrt{2}$ |
分析 由已知的等式求出复数z,然后直接利用复数模的公式求模,根据共轭复数的定义,以及复数的概念判断即可.
解答 解:z=$\frac{2}{1-i}$=$\frac{2(1+i)}{(1-i)(1+i)}$=1+i,
∴z的实部为1,虚部为1,$\overline{z}$=1-i,|z|=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
故选:D.
点评 本题考查了复数代数形式的乘除运算,考查了复数模,共轭复数的求法,是基础的计算题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知实数1,t,4成等比数列,则圆锥曲线$\frac{x^2}{t}+{y^2}$=1的离心率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$或$\sqrt{3}$ | C. | $\frac{1}{2}$或$\sqrt{3}$ | D. | $\frac{{\sqrt{2}}}{2}$或3 |
12.如图,根据样本的频率分布直方图,估计样本的中位数是( )


| A. | 10 | B. | 12 | C. | 13 | D. | 16 |
9.已知$sin(\frac{π}{4}+α)$=$\frac{1}{3}$,则sin2α的值为( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $-\frac{7}{9}$ | D. | $\frac{7}{9}$ |
10.已知F1,F2分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,若点P是以F1F2为直径的圆与C右支的一个交点,PF1交C于另一点Q,且|PQ|=2|QF1|,则C的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
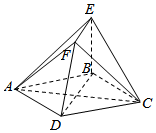 如图,四边形ABCD为菱形,EB⊥平面ABCD,EF∥BD,EF=$\frac{1}{2}$BD.
如图,四边形ABCD为菱形,EB⊥平面ABCD,EF∥BD,EF=$\frac{1}{2}$BD.