题目内容
6.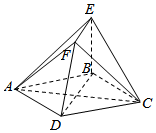 如图,四边形ABCD为菱形,EB⊥平面ABCD,EF∥BD,EF=$\frac{1}{2}$BD.
如图,四边形ABCD为菱形,EB⊥平面ABCD,EF∥BD,EF=$\frac{1}{2}$BD.(Ⅰ)求证:DF∥平面AEC;
(Ⅱ)求证:平面AEF⊥平面AFC.
分析 (I)设AC与BD的交点为O,连接EO,则四边形DOEF为平行四边形,故而DF∥OE,于是DF∥平面AEC;
(II)由BE⊥平面ABCD可得BE⊥BO,即四边形OBEF是矩形,于是OB⊥OF,由菱形的性质得OB⊥AC,故而OB⊥平面AFC,而OB∥EF,EF?平面AEF,故而平面AEF⊥平面AFC.
解答 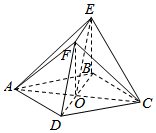 证明:(I)设AC与BD的交点为O,连接EO,
证明:(I)设AC与BD的交点为O,连接EO,
因为$EF=\frac{1}{2}BD$,所以EF=OD
因为EF∥BD,所以EF∥OD.
故四边形DOEF为平行四边形,
所以DF∥OE,
又OE?平面AEC,DF?平面AEC,
所以DF∥平面AEC.
(Ⅱ)连结OF,因为$EF=\frac{1}{2}BD$,所以EF=OB,因为EF∥BD,所以EF∥OB,
故四边形BOFE为平行四边形.
所以EB∥FO,因为EB⊥平面ABCD,所以FO⊥平面ABCD,
又OB?平面ABCD,所以FO⊥OB.
因为四边形ABCD为菱形,所以OB⊥AC,
又AC?平面AFC,OF?平面AFC,AC∩OF=O,
所以OB⊥平面AFC.
又EF∥OB,所以EF⊥平面AFC.
因为EF?平面AEF,
所以平面AEF⊥平面AFC.
点评 本题考查了线面平行,面面垂直的判定,属于中档题.

练习册系列答案
相关题目
17.已知集合A={0,1,2},B={x|x(x-2)<0},则A∩B( )
| A. | {0,1,2} | B. | {1,2} | C. | {0,1} | D. | {1} |
1.复数z=$\frac{2}{1-i}$(i为虚数单位),则( )
| A. | z的实部为2 | B. | z的虚部为i | C. | $\overline z$=1+i | D. | |z|=$\sqrt{2}$ |
11.如果实数x,y满足条件$\left\{\begin{array}{l}{2x+y-2≥0}\\{x-y+2≥0}\\{x-a≤0}\end{array}\right.$,若z=$\frac{y-1}{x+1}$的最小值小于$\frac{1}{2}$,则实数a的取值范围是( )
| A. | (-∞,1) | B. | (1,+∞) | C. | ($\frac{1}{5}$,1) | D. | ($\frac{1}{5}$,+∞) |
15.若实数x,y满足$\left\{\begin{array}{l}x-y-2≥0\\ 2x+y-2≤0\\ y+4≥0.\end{array}\right.$,则目标函数z=4x+3y的最大值为( )
| A. | 0 | B. | $\frac{10}{3}$ | C. | 12 | D. | 20 |