题目内容
如图，有一张长为8，宽为4的矩形纸片ABCD，按如图所示方法进行折叠，使每次折叠后点B都落在AD边上，此时记为B′（注：图中EF为折痕，点F也可落在CD边上）过点B′作B′T∥CD交EF于点T，求点T的轨迹方程．考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：以边AB的中点O为原点，AB边所在的直线为y轴建立平面直角坐标系，因为|BT|=|B′T|，B′T⊥AD，根据抛物线的定义，T点的轨迹是以点B为焦点，AD为准线的抛物线的一部分，利用|AB|=4，即定点B到定直线AD的距离为4，可得结论．
解答：
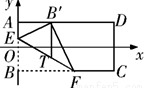解：如图，以边AB的中点O为原点，AB边所在的直线为y轴建立平面直角坐标系，则B（0，-2）．
因为|BT|=|B′T|，B′T⊥AD，根据抛物线的定义，T点的轨迹是以点B为焦点，AD为准线的抛物线的一部分．
设T（x，y），由|AB|=4，即定点B到定直线AD的距离为4．
所以抛物线的方程为x2=-8y．
在折叠中，线段AB′长度|AB′|在区间[0，4]内变化，而x=|AB′|，所以0≤x≤4．
故点T的轨迹方程为x2=-8y（0≤x≤4）．
解：如图，以边AB的中点O为原点，AB边所在的直线为y轴建立平面直角坐标系，则B（0，-2）．因为|BT|=|B′T|，B′T⊥AD，根据抛物线的定义，T点的轨迹是以点B为焦点，AD为准线的抛物线的一部分．
设T（x，y），由|AB|=4，即定点B到定直线AD的距离为4．
所以抛物线的方程为x2=-8y．
在折叠中，线段AB′长度|AB′|在区间[0，4]内变化，而x=|AB′|，所以0≤x≤4．
故点T的轨迹方程为x2=-8y（0≤x≤4）．
点评：本题主要考查抛物线的定义及标准方程，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
期末集结号系列答案
相关题目