题目内容
10.y=10x在(1,10)处切线的斜率为10ln10.分析 求出函数的导数,由导数的几何意义可得,代入x=1,即有函数在(1,10)处切线的斜率.
解答 解:y=10x的导数为y′=10xln10,
由导数的几何意义可得,
在(1,10)处切线的斜率为10ln10.
故答案为:10ln10.
点评 本题考查导数的运用:求切线的斜率,考查导数的几何意义:函数在某点处的导数即为曲线在该点处切线的斜率,考查运算能力,正确求导是解题的关键,属于基础题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
15.若等差数列{an}满足a8+a9+a10>0,a9+a10<0,则当n=( )时,{an}的前n项和最大.
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
20.曲线y=x3-$\sqrt{3}x$+2上的任意一点P处切线的倾斜角的取值范围是( )
| A. | [$\frac{π}{3}$,$\frac{π}{2}$) | B. | [$\frac{2π}{3}$,π) | C. | [0,$\frac{π}{2}$)∪($\frac{π}{2}$,$\frac{2π}{3}$] | D. | [0,$\frac{π}{2}$)∪[$\frac{2π}{3}$,π) |
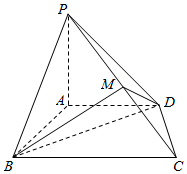 已知四棱锥P-ABCD中,PA垂直于直角梯形ABCD所在的平面,BA⊥AD,BC∥AD,M是PC的中点,且AB=AD=AP=2,BC=4.
已知四棱锥P-ABCD中,PA垂直于直角梯形ABCD所在的平面,BA⊥AD,BC∥AD,M是PC的中点,且AB=AD=AP=2,BC=4.