题目内容
已知向量
=(sinx,-1),
=(cosx,
),f(x)=(
+
)•
.
(1)当x∈[0,
]时,求函数f(x)的值域:
(2)锐角△ABC中,a,b,c分别为角A,B,C的对边,若f(
)=
,b=7
,a=
c,求边a,c.
| m |
| n |
| 3 |
| 2 |
| m |
| n |
| m |
(1)当x∈[0,
| π |
| 2 |
(2)锐角△ABC中,a,b,c分别为角A,B,C的对边,若f(
| B |
| 2 |
3
| ||
| 10 |
| 2 |
4
| ||
| 5 |
考点:平面向量数量积的运算,三角函数中的恒等变换应用,余弦定理
专题:计算题,三角函数的图像与性质,解三角形,平面向量及应用
分析:(1)运用向量的数量积的坐标表示和二倍角公式及两角差的正弦公式,化简函数f(x),再由x的范围,结合正弦函数的图象和性质,即可得到所求值域;
(2)运用角的变换和两角和的余弦公式,计算可得cosB,再由余弦定理,结合条件即可求得c,a的值.
(2)运用角的变换和两角和的余弦公式,计算可得cosB,再由余弦定理,结合条件即可求得c,a的值.
解答:
解:(1)由于
+
=(sinx+cosx,
),
则f(x)=(sinx+cosx)sinx-
=sin2x+sinxcosx-
=
sin2x-
cos2x=
(
sin2x-
cos2x)=
sin(2x-
),
当x∈[0,
]时,2x-
∈[-
,
],sin(2x-
)∈[-
,1]
则当x∈[0,
]时,函数f(x)的值域为[-
,
]:
(2)由f(
)=
,得sin(B-
)=
,
又B∈(0,
),即有B-
∈(-
,
),
则cos(B-
)=
=
,
即有cosB=cos[(B-
)+
]=cos(B-
)cos
-sin(B-
)sin
=
×
-
×
=
,
由余弦定理b2=a2+c2-2accosB,得
98=
c2+c2-2×
c2×
,
解得c=5
,a=
×5
=8.
| m |
| n |
| 1 |
| 2 |
则f(x)=(sinx+cosx)sinx-
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| π |
| 4 |
当x∈[0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| ||
| 2 |
则当x∈[0,
| π |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
(2)由f(
| B |
| 2 |
3
| ||
| 10 |
| π |
| 4 |
| 3 |
| 5 |
又B∈(0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
则cos(B-
| π |
| 4 |
1-
|
| 4 |
| 5 |
即有cosB=cos[(B-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
=
| 4 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
| ||
| 2 |
| ||
| 10 |
由余弦定理b2=a2+c2-2accosB,得
98=
| 32 |
| 25 |
4
| ||
| 5 |
| ||
| 10 |
解得c=5
| 2 |
4
| ||
| 5 |
| 2 |
点评:本题考查平面向量的数量积的坐标表示,考查二倍角和两角和差的正弦、余弦公式的运用,考查余弦定理,运用正弦函数的图象和性质以及角的变换是解题的关键.

练习册系列答案
相关题目
已知|
|=6,|
|=8,
•
=22,则|
+
|为( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、10 | B、12 | C、72 | D、144 |
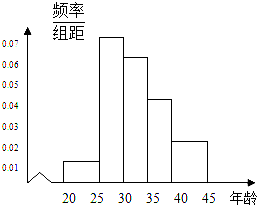 南昌市为增强市民的交通安全意识,面向全市征召“小红帽”志愿者在部分交通路口协助交警维持交通,把符合条件的1000名志愿者按年龄分组:第1组[20,25)、第2组[25,30)、第3组[30,35)、第4组[35,40)、第5组[40,45),得到的频率分布直方图如图所示:
南昌市为增强市民的交通安全意识,面向全市征召“小红帽”志愿者在部分交通路口协助交警维持交通,把符合条件的1000名志愿者按年龄分组:第1组[20,25)、第2组[25,30)、第3组[30,35)、第4组[35,40)、第5组[40,45),得到的频率分布直方图如图所示: