题目内容
已知函数y=f（x）是R上的偶函数，对于x∈R都有f（x+6）=f（x）+f（3）成立，当x1，x2∈[0，3]，且x1≠x2，都有
＞0，方程f（x）=0在[-9，9]上根的个数为 ．
| f(x2)-f(x1) |
| x2-x1 |
考点：函数奇偶性的性质,根的存在性及根的个数判断
专题：函数的性质及应用
分析：先根据偶函数性质，利用赋值法可求出f（3）的值，进一步确定出函数f（x）的周期为6，然后结合x1≠x2，都有
＞0，可得函数的单调性，综合以上因素即可获解．
| f(x2)-f(x1) |
| x2-x1 |
解答：
解：因为y=f（x）是R上的偶函数，对于x∈R都有f（x+6）=f（x）+f（3）成立，
所以f（-3+6）=f（-3）+f（3），且f（-3）=f（3），所以f（3）=0．
故f（x+6）=f（x），故该函数的周期为6．
由且x1≠x2，都有
＞0可知，函数f（x）在[0，3]上递增，结合偶函数的性质，所以f（x）在[-3，0]上递减．
所以在[-9，9]上只有f（-9）=f（-3）=f（3）=f（9）=0．
故f（x）=0在[-9，9]上根的个数为4．
故答案为：4．
所以f（-3+6）=f（-3）+f（3），且f（-3）=f（3），所以f（3）=0．
故f（x+6）=f（x），故该函数的周期为6．
由且x1≠x2，都有
| f(x2)-f(x1) |
| x2-x1 |
所以在[-9，9]上只有f（-9）=f（-3）=f（3）=f（9）=0．
故f（x）=0在[-9，9]上根的个数为4．
故答案为：4．
点评：本题考查了函数的奇偶性、周期性以及单调性的综合应用，属于中档题，注意转化思想的应用．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
函数y=2sinx的单调增区间是（k∈Z）（ ）
A、[
| ||||
B、[-
| ||||
| C、[2kπ，π+2kπ] | ||||
D、[2kπ，
|
若等差数列{an}的前n项和为Sn，a4=4，S4=10则数列{
}的前2015项和为（ ）
| 1 |
| anan+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
某流程图如图所示，现输入如下四个函数，则可以输出的函数是（ ）
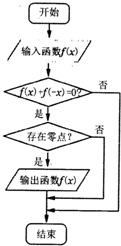
A、f（x）=
| ||||||
B、f（x）=
| ||||||
C、f（x）=
| ||||||
| D、f（x）=x2ln（x2+1） |