题目内容
解关于x的不等式：2|x-3|+|x-4|＜2．
考点：绝对值不等式的解法
专题：计算题,分类讨论,不等式的解法及应用
分析：运用零点分区间方法，讨论当x≥4时，当3＜x＜4时，当x≤3时，去绝对值，解不等式，最后求并集即可．
解答：
解：当x≥4时，原不等式即为2（x-3）+（x-4）＜2，即3x-10＜2，解得x＜4，则有x∈∅；
当3＜x＜4时，原不等式即为2（x-3）+（4-x）＜2，即x-2＜2，解得，x＜4，则有3＜x＜4；
当x≤3时，原不等式即为2（3-x）+（4-x）＜2，即10-3x＜2，解得，x＞
，则有
＜x≤3．
则原不等式的解集为{x|
＜x≤3或3＜x＜4}={x|
＜x＜4}．
当3＜x＜4时，原不等式即为2（x-3）+（4-x）＜2，即x-2＜2，解得，x＜4，则有3＜x＜4；
当x≤3时，原不等式即为2（3-x）+（4-x）＜2，即10-3x＜2，解得，x＞
| 8 |
| 3 |
| 8 |
| 3 |
则原不等式的解集为{x|
| 8 |
| 3 |
| 8 |
| 3 |
点评：本题考查绝对值不等式的解法，考查分类讨论的思想方法，考查运算能力，属于基础题．
练习册系列答案
相关题目
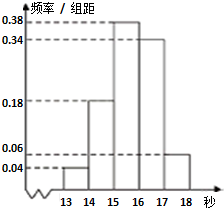南山中学高二某班50名学生在一次百米测试中，成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15）…，第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．