题目内容
函数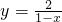 在区间[2,6]上的最大值和最小值分别是________.
在区间[2,6]上的最大值和最小值分别是________.
- ,-2
,-2
分析:先证明函数的单调性,用定义法,由于函数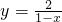 在区间[2,6]上是增函数,故最大值在右端点取到,最小值在左端点取到,求出两个端点的值即可.
在区间[2,6]上是增函数,故最大值在右端点取到,最小值在左端点取到,求出两个端点的值即可.
解答:设x1、x2是区间[2,6]上的任意两个实数,且x1<x2,则
f(x1)-f(x2)=-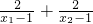
=-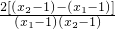
=-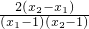 .
.
由2<x1<x2<6,得x2-x1>0,(x1-1)(x2-1)>0,
于是f(x1)-f(x2)<0,即f(x1)<f(x2).
所以函数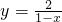 是区间[2,6]上的增函数,
是区间[2,6]上的增函数,
因此,函数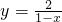 在区间的两个端点上分别取得最大值与最小值,
在区间的两个端点上分别取得最大值与最小值,
即当x=2时,ymin=-2;当x=6时,ymax=- .
.
故答案为:- ,-2
,-2
点评:本题考查函数的单调性,用单调性求最值是单调性的最重要的应用,属于基础题.
 ,-2
,-2分析:先证明函数的单调性,用定义法,由于函数
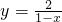 在区间[2,6]上是增函数,故最大值在右端点取到,最小值在左端点取到,求出两个端点的值即可.
在区间[2,6]上是增函数,故最大值在右端点取到,最小值在左端点取到,求出两个端点的值即可.解答:设x1、x2是区间[2,6]上的任意两个实数,且x1<x2,则
f(x1)-f(x2)=-
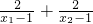
=-
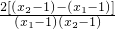
=-
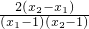 .
.由2<x1<x2<6,得x2-x1>0,(x1-1)(x2-1)>0,
于是f(x1)-f(x2)<0,即f(x1)<f(x2).
所以函数
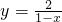 是区间[2,6]上的增函数,
是区间[2,6]上的增函数,因此,函数
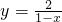 在区间的两个端点上分别取得最大值与最小值,
在区间的两个端点上分别取得最大值与最小值,即当x=2时,ymin=-2;当x=6时,ymax=-
 .
.故答案为:-
 ,-2
,-2点评:本题考查函数的单调性,用单调性求最值是单调性的最重要的应用,属于基础题.

练习册系列答案
相关题目
 设函数f(x)=|x2-4x-5|,x∈R.
设函数f(x)=|x2-4x-5|,x∈R.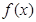 在区间[2,6]上是增函数,且最小值为4,则
在区间[2,6]上是增函数,且最小值为4,则