题目内容
8. 如图所示,MA⊥平面ABCD,底面ABCD边长为1的正方形,MA=2AB,P是MC上一点,且$\overrightarrow{CP}$=$\frac{1}{5}$$\overrightarrow{CM}$
如图所示,MA⊥平面ABCD,底面ABCD边长为1的正方形,MA=2AB,P是MC上一点,且$\overrightarrow{CP}$=$\frac{1}{5}$$\overrightarrow{CM}$(1)建立适当的坐标系并求点P坐标;
(2)求证:MB⊥DP.
分析 (1)以A为原点,AB为x轴,AD为y轴,AM为z轴,建立空间直角坐标系,能求出点P坐标.
(2)求出$\overrightarrow{MB}$,$\overrightarrow{DP}$,由∴$\overrightarrow{MB}•\overrightarrow{DP}$=0,能证明MB⊥DP.
解答 解:(1)∵MA⊥平面ABCD,底面ABCD边长为1的正方形,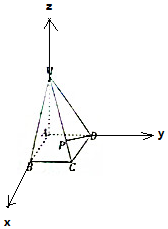
∴以A为原点,AB为x轴,AD为y轴,AM为z轴,建立空间直角坐标系,
∵MA=2AB,P是MC上一点,且$\overrightarrow{CP}$=$\frac{1}{5}$$\overrightarrow{CM}$,
∴C(1,1,0),M(0,0,2),设P(a,b,c),
则由$\overrightarrow{CP}$=$\frac{1}{5}$$\overrightarrow{CM}$,得(a-1,b-1,c)=(-$\frac{1}{5}$,-$\frac{1}{5}$,$\frac{2}{5}$),
∴$\left\{\begin{array}{l}{a-1=-\frac{1}{5}}\\{b-1=-\frac{1}{5}}\\{c=\frac{2}{5}}\end{array}\right.$,解得a=$\frac{4}{5}$,b=$\frac{4}{5}$,c=$\frac{2}{5}$,
∴点P坐标($\frac{4}{5},\frac{4}{5},\frac{2}{5}$).
证明:(2)B(1,0,0),D(0,1,0),
$\overrightarrow{MB}$=(1,0,-2),$\overrightarrow{DP}$=($\frac{4}{5}$,-$\frac{1}{5}$,$\frac{2}{5}$),
∴$\overrightarrow{MB}•\overrightarrow{DP}$=$\frac{4}{5}+0-\frac{4}{5}$=0,
∴MB⊥DP.
点评 本题考查点的坐标的求法,考查线线垂直的证明,是基础题,解题时要认真审题,注意向量法的合理运用.

 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案| A. | (-∞,2) | B. | (-∞,3) | C. | (-∞,4) | D. | (-∞,5) |
| A. | 6 | B. | -2$\sqrt{3}$ | C. | -6 | D. | 2$\sqrt{3}$ |
 .
.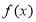 的最小值;
的最小值; 中,角
中,角 ,
, ,
,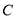 的对边分别是
的对边分别是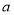 ,
, ,
, ,若
,若 ,
,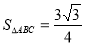 ,
, ,求
,求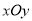 中,过点
中,过点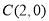 的直线与抛物线
的直线与抛物线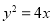 相交于点
相交于点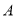 、
、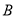 两点,设
两点,设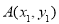 ,
,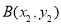 .
.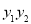 为定值;
为定值;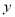 轴的定直线被以
轴的定直线被以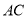 为直径的圆截得的弦长为定值?如果存在,求出该直线方程和弦长,如果不存在,说明理由.
为直径的圆截得的弦长为定值?如果存在,求出该直线方程和弦长,如果不存在,说明理由.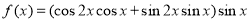 ,
,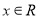 ,则
,则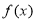 是( )
是( )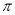 的奇函数 B.最小正周期为
的奇函数 B.最小正周期为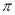 的偶函数
的偶函数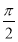 的奇函数 D.最小正周期为
的奇函数 D.最小正周期为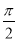 的偶函数
的偶函数