题目内容
已知函数f(x)=x2+ax-lnx,a∈R。
(1)若函数f(x)在上是减函数,求实数a的取值范围;
(2)令g(x)=f(x)-x2,是否存在实数a,当x∈(0,e](e是自然对数的底数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由.
解:(1)f′(x)=2x+a-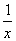 =
=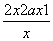 ≤0在上恒成立
≤0在上恒成立
令h(x)=2x2+ax-1,x∈,∴h(x)≤0在上恒成立
∴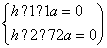 得
得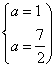 ,∴a≤-
,∴a≤-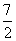 . --------5分
. --------5分
(2)假设存在实数a,使g(x)=f(x)-x2,x∈(0,e]有最小值3
g(x)=ax-lnx,x∈(0,e],g′(x)=a-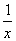 =
=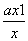
①当a≤0时,g′(x)<0,g(x)在(0,e]上单调递减
∴g(x)min=g(e)=ae-1=3,∴a=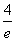 (舍去)
(舍去)
②当0<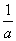 <e即a>
<e即a> 时,在(0,
时,在(0,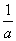 )上,g′(x)<0;在(
)上,g′(x)<0;在(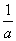 ,e]上,g′(x)>0
,e]上,g′(x)>0
∴g(x)在(0,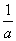 ]上单调递减,在(
]上单调递减,在(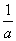 ,e]上单调递增
,e]上单调递增
∴g(x)min=g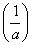 =1+lna=3,∴a=e2满足条件
=1+lna=3,∴a=e2满足条件
③当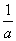 ≥e即0<a≤
≥e即0<a≤ 时,g′(x)<0,g(x)在(0,e]上单调递减
时,g′(x)<0,g(x)在(0,e]上单调递减
g(x)min=g(e)=ae-1=3
∴a=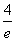 >
> (舍去)
(舍去)
综上所述:a=e2 --------10分

练习册系列答案
相关题目
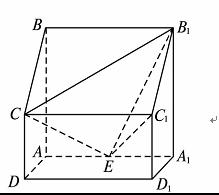
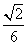 ,求线段AM的长.
,求线段AM的长. .
. ,求△ABC的面积S
,求△ABC的面积S 的最大值等于 ( )
的最大值等于 ( ) B.
B. 
 D.
D. 
 ,复数
,复数 ,
, ”是“一元二次不等式
”是“一元二次不等式 的解集为R”的
的解集为R”的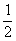 ,纵坐标不变;
,纵坐标不变;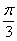 个单位;④图象向左平移
个单位;④图象向左平移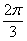 个单位;⑥图象向左平移
个单位;⑥图象向左平移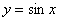 的图象变换到函数
的图象变换到函数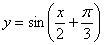 的图象,那么这两种变换的序号依次是_______
的图象,那么这两种变换的序号依次是_______ 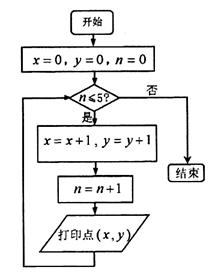
 ,曲线
,曲线 以及
以及 所围成的图形的面积为( )
所围成的图形的面积为( ) B.
B. C.
C. D.16
D.16  ,
, ,则
,则 =
= B.
B. C.
C. D.
D.