题目内容
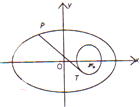 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
(1)当l经过原点时,l的斜率为-
| ||
| 3 |
(2)若|PT|的最小值不小于
| ||
| 2 |
考点:直线与圆锥曲线的关系,椭圆的标准方程,椭圆的简单性质
专题:计算题,直线与圆,圆锥曲线中的最值与范围问题
分析:(1)由题意可得
=
=
,从而解出a,b,c;从而求椭圆的方程;
(2)由题意可得直线m的方程为y=k(x-1),联立方程得到
,从而可得(a2k2+1)x2-2a2k2x+a2k2-a2=0;由韦达定理,设A(x1,y1),B(x2,y2),则有x1+x2=
,x1x2=
;
则由OA⊥OB得
•
=0,即x1x2+y1y2=
=0,从而可得k=a;利用两点间的距离公式求解即可.
| b-c |
| c |
| 1-c |
| c |
| 1 |
| 2 |
(2)由题意可得直线m的方程为y=k(x-1),联立方程得到
|
| 2a2k2 |
| a2k2+1 |
| a2k2-a2 |
| a2k2+1 |
则由OA⊥OB得
| OA |
| OB |
| k2-a2 |
| a2k2+1 |
解答:
解:(1)当l经过原点时的斜率为-
,
故
=
=
,
解得,c=
;
故a2=b2+c2=1+
=
;
故椭圆方程为
+y2=1;
(2)由题意,点Q的坐标为(1,0),则得直线m的方程为y=k(x-1),
联立方程组
得,
(a2k2+1)x2-2a2k2x+a2k2-a2=0;
设A(x1,y1),B(x2,y2),则有x1+x2=
,x1x2=
;
代入直线方程得y1y2=
,x1x2+y1y2=
;
由题意OA⊥OB,所以
•
=0,
所以x1x2+y1y2=
=0,
所以k=a,直线m方程为ax-y-a=0,
圆心F2(c,0)到直线m的距离d=
.
CD2=4[(b-c)2-d2]=
;
|CD|=
=2
=2
,
根据题意可设切线长|PT|=
,
所以当且仅当|PF2|取得最小值时|PT|取得最小值,
而|PF2|min=a-c,
所以
≥
(a-c);.
所以0<
≤
,
从而解得
≤
,
解得,c≥
;
所以
≤c<1,
所以
≤2c+1<3;
则|CD|∈(0,
].
所以当c=
时,|CD|max=
.
| ||
| 3 |
故
| b-c |
| c |
| 1-c |
| c |
| 1 |
| 2 |
解得,c=
| 2 |
| 3 |
故a2=b2+c2=1+
| 4 |
| 9 |
| 13 |
| 9 |
故椭圆方程为
| 9x2 |
| 13 |
(2)由题意,点Q的坐标为(1,0),则得直线m的方程为y=k(x-1),
联立方程组
|
(a2k2+1)x2-2a2k2x+a2k2-a2=0;
设A(x1,y1),B(x2,y2),则有x1+x2=
| 2a2k2 |
| a2k2+1 |
| a2k2-a2 |
| a2k2+1 |
代入直线方程得y1y2=
| k2(1-a2) |
| a2k2+1 |
| k2-a2 |
| a2k2+1 |
由题意OA⊥OB,所以
| OA |
| OB |
所以x1x2+y1y2=
| k2-a2 |
| a2k2+1 |
所以k=a,直线m方程为ax-y-a=0,
圆心F2(c,0)到直线m的距离d=
| |ac-a| | ||
|
CD2=4[(b-c)2-d2]=
| 4(c-1)2 |
| a2+1 |
|CD|=
| 2|c-1| | ||
|
|
1-
|
根据题意可设切线长|PT|=
| |PF2|2-(b-c)2 |
所以当且仅当|PF2|取得最小值时|PT|取得最小值,
而|PF2|min=a-c,
所以
| (a-c)2-(b-c)2 |
| ||
| 2 |
所以0<
| b-c |
| a-c |
| 1 |
| 2 |
从而解得
| 1-c | ||
|
| 1 |
| 2 |
解得,c≥
| 3 |
| 4 |
所以
| 3 |
| 4 |
所以
| 5 |
| 2 |
则|CD|∈(0,
2
| ||
| 41 |
所以当c=
| 3 |
| 4 |
2
| ||
| 41 |
点评:本题考查了圆锥曲线与直线的应用,化简很复杂,属于难题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知c<0,在下列不等式中成立的是( )
| A、2c>1 | ||
B、c>(
| ||
C、2c<(
| ||
D、2c>(
|
若0<x<
,则x(1-2x)有( )
| 1 |
| 2 |
A、最小值
| ||
B、最小值
| ||
C、最大值
| ||
D、最大值
|
 如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是
如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是