题目内容
12.已知x∈($\frac{π}{2}$,π),sinx=$\frac{3}{5}$,则tan(π+2x)=$-\frac{24}{7}$.分析 利用同角三角函数的基本关系,求出 cosx、tanx,再利用二倍角的正切公式求出tan2x 的值.
解答 解:∵x∈($\frac{π}{2}$,π),sinx=$\frac{3}{5}$,
∴cosx=-$\sqrt{1-(\frac{3}{5})^{2}}$=-$\frac{4}{5}$,tanx=$\frac{sinx}{cosx}$=-$\frac{3}{4}$,
∴tan(π+2x)=tan2x=$\frac{2tanx}{1-ta{n}^{2}x}$=$\frac{2×(-\frac{3}{4})}{1-(-\frac{3}{4})^{2}}$=$-\frac{24}{7}$.
故答案是:$-\frac{24}{7}$.
点评 本题考查同角三角函数的基本关系,以及二倍角的正切公式的应用,求出cosx值是解题的关键.

练习册系列答案
相关题目
2.运行如图的程序,若x=2,则输出的y等于( )


| A. | 9 | B. | 7 | C. | 13 | D. | 11 |
3.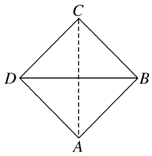 已知正四面体(所有棱长都相等的三棱锥)的俯视图如图所示,其中四边形ABCD是边长为$\sqrt{2}$cm的正方形,则这个正四面体的主视图的面积为( )cm2.
已知正四面体(所有棱长都相等的三棱锥)的俯视图如图所示,其中四边形ABCD是边长为$\sqrt{2}$cm的正方形,则这个正四面体的主视图的面积为( )cm2.
 已知正四面体(所有棱长都相等的三棱锥)的俯视图如图所示,其中四边形ABCD是边长为$\sqrt{2}$cm的正方形,则这个正四面体的主视图的面积为( )cm2.
已知正四面体(所有棱长都相等的三棱锥)的俯视图如图所示,其中四边形ABCD是边长为$\sqrt{2}$cm的正方形,则这个正四面体的主视图的面积为( )cm2.| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
4.函数f(x)=$\frac{{x}^{2}+5}{\sqrt{{x}^{2}+4}}$(x∈R)的最小值为( )
| A. | 2 | B. | 3 | C. | 2$\sqrt{2}$ | D. | 2.5 |
2.已知p:|1-$\frac{x-1}{3}$|≤2,q:x2-2x+1-m2≤0(m>0),若¬p是¬q的必要不充分条件,则实数m的取值范围为( )
| A. | m>9 | B. | m≥9 | C. | m≥7 | D. | m>7 |
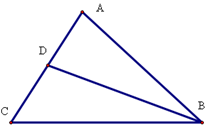 在△ABC中,角A、B、C所对的边分别为a,b,c,B=45°,AC=$\sqrt{5}$,cosC=$\frac{{\sqrt{5},}}{5}$,求
在△ABC中,角A、B、C所对的边分别为a,b,c,B=45°,AC=$\sqrt{5}$,cosC=$\frac{{\sqrt{5},}}{5}$,求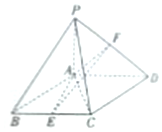 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,AB=2,PA=$\frac{{2\sqrt{3}}}{3}$,E为BC中点,F在棱PD上,AF⊥PD,点B到平面AEF的距离为$\frac{\sqrt{3}}{2}$.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,AB=2,PA=$\frac{{2\sqrt{3}}}{3}$,E为BC中点,F在棱PD上,AF⊥PD,点B到平面AEF的距离为$\frac{\sqrt{3}}{2}$.
