题目内容
已知数列{an}为等差数列,公差d≠0,an≠0,(n∈N*),且akx2+2ak+1x+ak+2=0(k∈N*)
(1)求证:当k取不同自然数时,此方程有公共根;
(2)若方程不同的根依次为x1,x2,…,xn,…,求证:数列{
}为等差数列.
(1)求证:当k取不同自然数时,此方程有公共根;
(2)若方程不同的根依次为x1,x2,…,xn,…,求证:数列{
| 1 |
| 1+xn |
考点:等差关系的确定,数列递推式
专题:等差数列与等比数列
分析:(1)依题意,2ak+1=ak+ak+2,于是原方程可转化为(akx+ak+2)(x+1)=0,从而可证结论;
(2)原方程另一根为xn,利用韦达定理,可求得xn=-1-
,继而得
=-
,利用等差数列的定义,证明即可.
(2)原方程另一根为xn,利用韦达定理,可求得xn=-1-
| 2d |
| ak |
| 1 |
| 1+xn |
| ak |
| 2d |
解答:
证明:(1)∵{an}是等差数列,∴2ak+1=ak+ak+2,故方程akx2+2ak+1x+ak+2=0,
可变为(akx+ak+2)(x+1)=0,
∴当k取不同自然数时,原方程有一个公共根-1.
(2)原方程另一根为xn,则-xn=
=
=1+
,
∴xn=-1-
,1+xn=-
,
=-
,…(10分)
∴
-
=-
-(-
)=
=
=-
(常数).
∴数列{
}是以-
为公差的等差数列
可变为(akx+ak+2)(x+1)=0,
∴当k取不同自然数时,原方程有一个公共根-1.
(2)原方程另一根为xn,则-xn=
| ak+2 |
| ak |
| ak+2d |
| ak |
| 2d |
| ak |
∴xn=-1-
| 2d |
| ak |
| 2d |
| ak |
| 1 |
| 1+xn |
| ak |
| 2d |
∴
| 1 |
| 1+xn+1 |
| 1 |
| 1+xn |
| ak+1 |
| 2d |
| ak |
| 2d |
| ak-ak+1 |
| 2d |
| -d |
| 2d |
| 1 |
| 2 |
∴数列{
| 1 |
| 1+xn |
| 1 |
| 2 |
点评:本题考查等差关系得确定,考查方程思想与推理运算能力,属于中档题.

练习册系列答案
相关题目
O为坐标原点,F为抛物线C:y2=4x的焦点,P为C上一点,若∠OFP=120°,S△POF=( )
A、
| ||||||
B、2
| ||||||
C、
| ||||||
D、
|
设x=
+2
,y=3-
,集合M={m|m=a+b
,a∈Q,b∈Q},那么x,y与集合M的关系是( )
| 1 |
| 3 |
| 2 |
| 2 |
| 2 |
| A、x∈M y∈M |
| B、x∈M y∉M |
| C、x∉M y∈M |
| D、x∉M y∉M |
下列函数在(0,+∞)上是增函数的是( )
| A、y=9-x2 | ||
| B、y=x•log0.23+1 | ||
C、y=x
| ||
D、y=
|
设f(x)是R上的偶函数,且在[0,+∞)上是增函数,又f(1)=0,则满足f(log2x)>0的x的取值范围是( )
| A、(2,+∞) | ||
B、(0,
| ||
C、(0,
| ||
D、(
|
在(
+
)12的展开式中,x项的系数为( )
| x |
| 1 | |||
|
A、C
| ||
B、C
| ||
C、C
| ||
D、C
|
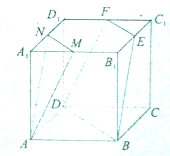 棱长为a的正方体ABCD-A1B1C1D1中,M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.
棱长为a的正方体ABCD-A1B1C1D1中,M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.