题目内容
函数f(x)=
+cosx在[0,+∞)内( )
| x |
| A、有无穷多个零点 |
| B、没有零点 |
| C、有且仅有一个零点 |
| D、有且仅有两个零点 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:通过讨论x的范围,确定
,cosx的范围,从而确定f(x)的符号,问题得解.
| x |
解答:
解:当x∈[0,
)时,
≥0,cosx>0,
∴f(x)>0,无零点,
当x∈[
,+∞)时,
≥
>1,-1≤cosx≤1,
∴f(x)>0,无零点,
故选:B.
| π |
| 2 |
| x |
∴f(x)>0,无零点,
当x∈[
| π |
| 2 |
| x |
|
∴f(x)>0,无零点,
故选:B.
点评:本题考察了函数的零点问题,渗透了分类讨论思想,是一道基础题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
直线x-y+1=0与圆x2+(y+1)2=2的位置关系是( )
| A、相离 | B、相切 |
| C、相交 | D、不能确定 |
如果复数(m-i)i(其中m∈R)的实部与虚部互为相反数,则m=( )
| A、2 | B、-2 | C、-1 | D、1 |
复数z=3+4i,|z|为复数z的模,
为复数z的共轭复数,i是虚数单位,则下列结论正确的是( )
. |
| z |
| A、z2>0 | ||
B、z•
| ||
| C、|z|=25 | ||
D、
|
已知实数x,y满足
,则目标函数z=2x-y的最大值为( )
|
| A、0 | B、3 | C、4 | D、6 |
观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a8+b8=( )
| A、28 | B、47 | C、76 | D、123 |
已知集合M={y|y=2cosx}.N={x|
≤0}.则集合M∩N=( )
| x+1 |
| x-2 |
| A、{x|-2≤x≤-1} |
| B、{x|-1≤x≤2} |
| C、{x|-1≤x<2} |
| D、{x|-1<x≤2} |
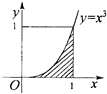 如图,设区域D={(x,y)|0≤x≤1,0≤y≤1},向区域D内随机投一点,且投入到区域内任一点都是等可能的,则点落入到阴影区域M={(x,y)|0≤x≤1,0≤y≤x3}的概率为
如图,设区域D={(x,y)|0≤x≤1,0≤y≤1},向区域D内随机投一点,且投入到区域内任一点都是等可能的,则点落入到阴影区域M={(x,y)|0≤x≤1,0≤y≤x3}的概率为