题目内容
已知圆O的半径为R,A、B是其圆周上的两个三等分点,则
•
的值为( )
| OA |
| OB |
分析:由题意求出两个向量的夹角,直接利用向量的数量积运算即可.
解答:解:因为圆O的半径为R,A、B是其圆周上的两个三等分点,
所以|
|=|
|=R,<
,
>=
,
所以
•
=|
|•|
|cos<
,
>=R2cos
=-
R2.
故选D,
所以|
| OA |
| OB |
| OA |
| OB |
| 2π |
| 3 |
所以
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| 2π |
| 3 |
| 1 |
| 2 |
故选D,
点评:本题考查平面向量的数量积的运算,求出两个向量的夹角是解题的关键,考查计算能力.

练习册系列答案
相关题目
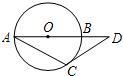 已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连接AC,若∠CAB=30°,求BD的长.
已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连接AC,若∠CAB=30°,求BD的长.