题目内容
已知圆O的半径为R,圆内一定点M且|MO|=
,一直线过点M且与该圆交于A,B 两点,则△OAB面积的最大值为
.
| R |
| 2 |
| ||
| 4 |
| ||
| 4 |
分析:以OM为y轴,建立直角坐标系,过点O作OD⊥AB,交AB于D,设直线AB的方程为y=kx+
,A(x1,y1),B(x2,y2),则△OAB面积S=
OM×|x1-x2|=
×|x1-x2|然后联立直线与圆的方程,求出|x1-x2|的最大值即可求出所求.
| R |
| 2 |
| 1 |
| 2 |
| R |
| 4 |
解答:解:以OM为y轴,建立直角坐标系 M(0,
M(0,
)
过点O作OD⊥AB,交AB于D
设直线AB的方程为y=kx+
,A(x1,y1),B(x2,y2)
则△OAB面积S=
OM×|x1-x2|=
×|x1-x2|
则x2+(kx+
)2=R2
∴(1+k2)x2+kRx-
=0
|x1-x2|2=(x1+x2)2-4x1•x2=
=
-
∴当k=0时|x1-x2|取最大值即S=
故答案为:
 M(0,
M(0,| R |
| 2 |
过点O作OD⊥AB,交AB于D
设直线AB的方程为y=kx+
| R |
| 2 |
则△OAB面积S=
| 1 |
| 2 |
| R |
| 4 |
|
| R |
| 2 |
∴(1+k2)x2+kRx-
| 3R2 |
| 4 |
|x1-x2|2=(x1+x2)2-4x1•x2=
| 4k2R2+3R2 |
| (1+k2)2 |
| 4R2 |
| k2+1 |
| R2 |
| (1+k2)2 |
∴当k=0时|x1-x2|取最大值即S=
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题主要考查了直线与圆的位置关系,以及函数的最值及其几何意义,同时考查了利用解析法求最值,属于中档题.

练习册系列答案
相关题目
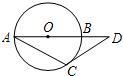 已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连接AC,若∠CAB=30°,求BD的长.
已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连接AC,若∠CAB=30°,求BD的长.