题目内容
已知圆O的半径为R,它的内接△ABC中,2R(sin2A-sin2C)=(| 2 |
分析:利用正弦定理把题设等式中的角的正弦转化成边,化简整理求得a,b和c的关系,继而代入余弦定理cosC中求得cosC的值,利用同角三角函数基本关系求得sinC,则利用三角形面积公式表示三角形的面积化简整理,根据A的范围确定面积的最大值.
解答:解:由已知得(2R)2(sin2A-sin2C)=2RsinB(
a-b),
即a2-c2=
ab-b2.
∴cosC=
=
,
∴C=
.S=
absinC=
ab=
•4R2sinAsinB=
R2sinAsin(
-A)
=
R2sinA(
cosA+
sinA)=R2(sinAcosA+sin2A)
=R2(
sin2A+
)=R2[
sin(2A-
)+
]≤
R2
∴当A=
时,面积S有最大值
R2.
| 2 |
即a2-c2=
| 2 |
∴cosC=
| a2+b2-c2 |
| 2ab |
| ||
| 2 |
∴C=
| π |
| 4 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
| 2 |
| 3π |
| 4 |
=
| 2 |
| ||
| 2 |
| ||
| 2 |
=R2(
| 1 |
| 2 |
| 1-cos2A |
| 2 |
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
1+
| ||
| 2 |
∴当A=
| 3π |
| 8 |
1+
| ||
| 2 |
点评:本题主要考查了余弦定理和正弦定理的应用.正弦定理和余弦定理及其变形公式是解三角形问题中常用的公式,故应熟练记忆.

练习册系列答案
相关题目
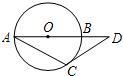 已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连接AC,若∠CAB=30°,求BD的长.
已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连接AC,若∠CAB=30°,求BD的长.