Question

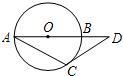已知圆O的半径为R，AB是圆O的直径，D是AB延长线上一点，DC是圆O的切线，C是切点，连接AC，若∠CAB=30°，求BD的长．

Answer 1

分析：先利用“同弧所对的圆周角是圆心角的一半”得出∠COD=2∠A=60°再解直角三角形可得CD长，最后用切割线定理可得BD长．

解答：解：连接OC，BC，
∵AB是圆O的直径，DC是圆O的切线，C是切点，
∴∠ACB=∠OCD=90°，
∵∠CAB=30°，
∴∠COD=2∠A=60°，CD=OC•tan∠COD=

3

R，
由切割线定理得，CD²=BD•AD=BD（BD+AB），
∴BD=R．
故BD的长为R．

点评：本题利用了直径对的圆周角是直角，切线的性质，切割线定理求解．本题主要考查与圆有关的比例线段、圆中的切割线定理，属于基础题．