题目内容
已知圆x2+y2=1及以下三个函数：（1）f（x）=x3；（2）f（x）=xcosx；（3）f（x）=tanx．其中图象能等分圆的面积的函数个数为（ ）
| A、3 | B、2 | C、1 | D、0 |
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：若图象能等分圆的面积，则等价为函数为奇函数，关于原点对称即可．
解答：
解：若函数图象能等分圆的面积，则函数为奇函数，
则：（1）f（x）=x3；为奇函数，满足条件．
（2）f（x）=xcosx；为奇函数，满足条件．
（3）f（x）=tanx．为奇函数，满足条件，
故选：A
则：（1）f（x）=x3；为奇函数，满足条件．
（2）f（x）=xcosx；为奇函数，满足条件．
（3）f（x）=tanx．为奇函数，满足条件，
故选：A
点评：本题主要考查函数奇偶性的判断，比较基础．
练习册系列答案
应用题作业本系列答案
相关题目
已知命题p：直线m，n相交，命题q：直线m，n异面，则?p是q成立的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
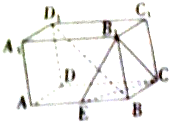如图所示，长方体ABCD-A1B1C1D1的侧面BCC1B1是正方形，E是AB的中点，AB=