题目内容
18．当x∈A时，若x-1∉A，x+1∉A，则称x为A的一个“孤立元素”，所有孤立元素组成的集合称为“孤星集”，求由集合A={0，1，2，3，5}中的“孤立元素”组成的“孤星集”．分析 由孤星集得出集合A={0，1，2，3，5}中的“孤立元素”组成的“孤星集”．
解答 解：由孤星集的定义可知，
集合A={0，1，2，3，5}中的“孤立元素”组成的“孤星集”是{5}．
点评 本题考查并集及其运算，是基础题．解题时要认真审题，仔细解答，注意熟练掌握孤星集的概念．
练习册系列答案
全能测控一本好卷系列答案
发散思维新课堂系列答案
相关题目
6．
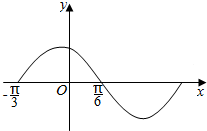函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的部分图象如图所示，如果x1，x2∈（-$\frac{π}{3}$，$\frac{π}{6}$），且f（x1）=f（x2），则f（x1+x2）等于（ ）
函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的部分图象如图所示，如果x1，x2∈（-$\frac{π}{3}$，$\frac{π}{6}$），且f（x1）=f（x2），则f（x1+x2）等于（ ）| A． | -1 | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | 1 |
4．函数f（x）是定义域在R上的偶函数，且f（x）=-f（2-x），若f（x）在区间[1，2]上是减函数，则f（x）（ ）
| A． | 在区间[-2，-1]上是增函数，在区间[3，4]上是增函数 | |
| B． | 在区间[-2，-1]上是增函数，在区间[3，4]上是减函数 | |
| C． | 在区间[-2，-1]上是减函数，在区间[3，4]上是增函数 | |
| D． | 在区间[-2，-1]上是减函数，在区间[3，4]上是减函数 |