题目内容
8.若函数y=f(x)满足以下条件:①对于任意的x∈R,y∈R,恒有f(x+y)=f(x)•f(y);②x∈(0,+∞)时,f(x)∈(1,+∞).(1)求f(0)的值;
(3)求证:f(x-y)=$\frac{f(x)}{f(y)}$(f(y)≠0);
(3)判断f(x)的单调性.
分析 (1)由题意可得f(x)•f(0)=f(x),解之即可求得f(0);
(2)利用f(x)=f[x-y+y]=f(x-y)f(y),即可证明结论;
(3)设x1,x2∈R且x1>x2,利用定义法作差,整理后即可证得差的符号,进而由定义得出函数的单调性.
解答 (1)解:由题意可得f(x)•f(0)=f(x)
∴f(0)=1;
(2)证明:f(x)=f[x-y+y]=f(x-y)f(y),
∵f(y)≠0,
∴f(x-y)=$\frac{f(x)}{f(y)}$;
(3)设x1,x2∈R且x1>x2,则f(x1)-f(x2)=f[(x1-x2)+x2]-f(x2)=f(x2)[f(x1-x2)-1]
∵x1-x2>0
∴f(x1-x2)>1
∴f(x1-x2)-1>0
对于任意x∈R,f(x)=f($\frac{x}{2}$+$\frac{x}{2}$)=[f($\frac{x}{2}$)]2≥0,
∵f($\frac{x}{2}$)≠0,∴f(x)>0
∴f(x2)>0
∴f(x2)f[(x1-x2)-1]>0
∴f(x1)>f(x2)故f(x)在R上是增函数
点评 本题考点是抽象函数及其应用,考查灵活赋值求值的能力以及灵活变形证明函数单调性的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.设l是空间一条直线,α和β是两个不同的平面,则下列结论正确的是( )
| A. | 若l∥α,l∥β,则α∥β | B. | 若α⊥β,l∥α,则l⊥β | C. | 若α⊥β,l⊥α,则l∥β | D. | 若l∥α,l⊥β,则α⊥β |
3.下列函数既是奇函数,又在区间[-1,1]上单调递增的是( )
| A. | y=sin2x | B. | y=-|x+1| | C. | y=ln$\frac{2+x}{2-x}$ | D. | y=$\frac{{a}^{x}+{a}^{-x}}{2}$ |
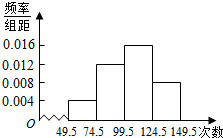 为了调查学生的课外阅读情况,在某班级对全体学生每天阅读时间(单位:分钟)进行调查,将调查数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第三组的频数为20.
为了调查学生的课外阅读情况,在某班级对全体学生每天阅读时间(单位:分钟)进行调查,将调查数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第三组的频数为20.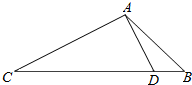 如图△ABC中,已知点D在BC边上,且AD⊥AC,sin∠BAC=$\frac{{2\sqrt{2}}}{3}$,AB=3$\sqrt{2}$,BD=$\sqrt{3}$.
如图△ABC中,已知点D在BC边上,且AD⊥AC,sin∠BAC=$\frac{{2\sqrt{2}}}{3}$,AB=3$\sqrt{2}$,BD=$\sqrt{3}$.