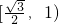题目内容
在正方体上任选3个顶点连成三角形，则所得的三角形是直角非等腰三角形的概率为
- A.
- B.
- C.
- D.
C
分析：由题意知本题是一个古典概型，总事件数是在正方体上任选3个顶点连成三角形可得C83个三角形，符合条件的要得直角非等腰三角形，则每个顶点上可得三个，即正方体的一边与过此点的一条面对角线，共有24个，由公式得到结果．
解答：在正方体上任选3个顶点连成三角形可得C83个三角形，
要得直角非等腰三角形，
则每个顶点上可得三个（即正方体的一边与过此点的一条面对角线），
共有24个，得P=
，
故选C．
点评：本题是一个古典概型，用排列组合数来求出事件的个数，排列组合问题在几何中的应用，在计算时要求做到，兼顾所有的条件，先排约束条件多的元素，做的不重不漏，注意实际问题本身的限制条件．
分析：由题意知本题是一个古典概型，总事件数是在正方体上任选3个顶点连成三角形可得C83个三角形，符合条件的要得直角非等腰三角形，则每个顶点上可得三个，即正方体的一边与过此点的一条面对角线，共有24个，由公式得到结果．
解答：在正方体上任选3个顶点连成三角形可得C83个三角形，
要得直角非等腰三角形，
则每个顶点上可得三个（即正方体的一边与过此点的一条面对角线），
共有24个，得P=
，故选C．
点评：本题是一个古典概型，用排列组合数来求出事件的个数，排列组合问题在几何中的应用，在计算时要求做到，兼顾所有的条件，先排约束条件多的元素，做的不重不漏，注意实际问题本身的限制条件．
练习册系列答案
相关题目
φ）（0＜φ＜π），且f（x）+f′（x）为奇函数．
，则A∩CRB=
为纯虚数，则a=________．
上有一点M，F1，F2是椭圆的两个焦点，若
，则椭圆离心率的范围是
