题目内容
10．不等式${2^{{x^2}+2x-4}}≤\frac{1}{2}$的解集为（ ）| A． | [-1，3] | B． | [-3，-1] | C． | [-3，1] | D． | [1，3] |
分析 根据指数函数的单调性，把原不等式化为${2}^{{x}^{2}+2x-4}$≤2-1，求出解集即可．
解答 解：不等式${2^{{x^2}+2x-4}}≤\frac{1}{2}$可化为${2}^{{x}^{2}+2x-4}$≤2-1，
即x2+2x-4≤-1，
整理得x2+2x-3≤0，
解得-3≤x≤1，
所以原不等式的解集为[-3，1]．
故选：C．
点评 本题考查了利用指数函数求不等式的解集的应用问题，是基础题目．
练习册系列答案
相关题目
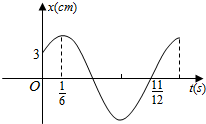如图，单摆从某点开始来回摆动，离开平衡位置的距离s（cm）和时间t（s）的函数关系是s=Asin（ωt+φ），0＜φ＜$\frac{π}{2}$，根据图象，求：
15．已知全集U={0，1，2，3，4}，P={x∈N|-1＜x＜3}，则P的补集∁UP=（ ）
| A． | {4} | B． | {0，4} | C． | {3，4} | D． | {0，3，4} |