Question

13．若f（x）是偶函数，定义域为{x∈R|x≠0}，且在（-∞，0）上是增函数，又f（-2）=0，求满足（x+1）f（x-1）＞0的x的取值范围．

Answer 1

分析 根据题意和偶函数的性质画出f（x）的单调性示意图，根据图象列出等价的不等式组，注意函数f（x）的定义域，求出不等式组的解集．

解答 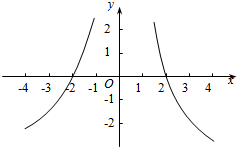解：由题意可得，函数f（x）的图象关于y轴对称，
f（x）在（-∞，0）上是增函数，且f（-2）=0，
函数f（x）的单调性示意图如图所示：
由（x+1）f（x-1）＞0 可得，
所以$\left\{\begin{array}{l}{x+1＜0}\\{f（x-1）＜0}\end{array}\right.$或$\left\{\begin{array}{l}{x+1＞0}\\{f（x-1）＞0}\end{array}\right.$，
则$\left\{\begin{array}{l}{x＜-1}\\{x-1＜-2}\end{array}\right.$或$\left\{\begin{array}{l}{x＞-1}\\{-2＜x-1＜0或0＜x-1＜2}\end{array}\right.$，
解得x＜-1或-1＜x＜2且x≠1，
所以x的取值范围是{x|x＜2且x≠1、x≠-1}．

点评 本题主要考查求函数的单调性和奇偶性的应用，体现了转化以及数形结合的数学思想，属于中档题．