题目内容
1．已知数列{an}满足an＞0，其前n项和为Sn满足2Sn=an2+an．则an=n．分析 通过当n≥2时2an=2Sn-2Sn-1计算、整理可知an+an-1=（an-an-1）（an+an-1），通过an＞0可知an+an-1＞0，从而an-an-1=1，进而可知数列{an}是以首项、公差均为1的等差数列，计算即得结论．
解答 解：∵2Sn=an2+an，
∴当n≥2时，2Sn-1=an-12+an-1，
∴2an=2Sn-2Sn-1
=（an2+an）-（an-12+an-1）
=${{a}_{n}}^{2}$-${{a}_{n-1}}^{2}$+an-an-1，
整理得：an+an-1=${{a}_{n}}^{2}$-an-1=（an-an-1）（an+an-1），
又∵an＞0，
∴an+an-1＞0，
∴an-an-1=1，
又∵2S1=a12+a1，
∴a1=1或a1=0（舍），
∴数列{an}是以首项、公差均为1的等差数列，
∴an=n，
故答案为：n．
点评 本题考查数列的通项，考查运算求解能力，注意解题方法的积累，属于中档题．
练习册系列答案
相关题目
11．sin95°sin35°+cos95°cos35°=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | -$\frac{1}{2}$ | D． | -$\frac{{\sqrt{3}}}{2}$ |
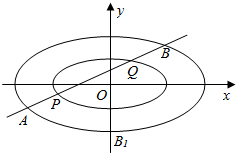已知椭圆C1，$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞1）与椭圆C2：$\frac{{x}^{2}}{4}$+y2=1有相同的离心率，经过点P（-2，0）的直线l与椭圆C2相交于P、Q两点，与椭圆C1相交于A、B两点．