题目内容
4．不等式|x+1|+|x-2|≥4a对任意实数x恒成立，则a的取值范围是（-∞，3]．分析 求出|x+1|+|x-2|的最小值，然后求解a的范围即可．
解答 解：因为|x+1|+|x-2|≥|x+1-x+2|=3，
不等式|x+1|+|x-2|≥4a对任意实数x恒成立，
可得4a≤3，解得a≤$\frac{3}{4}$．
a的取值范围是：（-∞，3]．
故答案为：（-∞，3]．
点评 本题考查函数恒成立，绝对值三角不等式的应用，考查计算能力．
练习册系列答案
快乐5加2金卷系列答案
相关题目
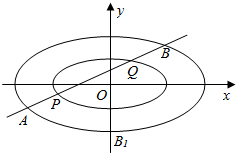已知椭圆C1，$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞1）与椭圆C2：$\frac{{x}^{2}}{4}$+y2=1有相同的离心率，经过点P（-2，0）的直线l与椭圆C2相交于P、Q两点，与椭圆C1相交于A、B两点．