题目内容
6. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{3}$AD,过BC的平面交PD于M,交PA于N(N与A不重合).
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{3}$AD,过BC的平面交PD于M,交PA于N(N与A不重合).(1)求证:MN∥BC;
(2)若PM=$\frac{1}{3}$PD,求证:AC⊥BM.
分析 (1)根据线面平行的性质定理即可证明MN∥BC;
(2)取AE=$\frac{1}{3}$AD,根据线面垂直的性质定理证明AC⊥BM.
解答 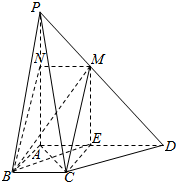 证明:(1)∵BC∥AD,BC?平面PAD,AD?平面PAD,
证明:(1)∵BC∥AD,BC?平面PAD,AD?平面PAD,
∴BC∥平面PAD,
∵平面PAD∩平面BCMN=MN,
∴BC∥MN,即MN∥BC;
(2)取AE=$\frac{1}{3}$AD,则ME∥PA,AE=AB.
∵PA⊥底面ABCD,
∴ME⊥底面ABCD,∴ME⊥AC,
∵BC∥AD,AB⊥AD,
∴ABCE是正方形,
∴AC⊥BE,
∵ME∩BE=E,
∴AC⊥平面MBE,
∵BM?平面MBE,
∴AC⊥BM.
点评 本题主要考查线面垂直和线面平行的判定和性质,综合考查空间直线和平面的位置关系的判定,要求熟练掌握相应的判定定理和性质定理,考查学生的运算和推理能力.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
14.汽车发动机排量可以分为两类,高于1.6L的称为大排量,否则称为小排量,加油时,有92号与95号两种汽油可供选择,某汽车网站的注册会员中,有300名老会员参与了网络调查,结果如下:
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
(1)根据此次调查,是否有95%的把握认为该网站会员给汽车加油时进行的型号选择与汽车排量有关?
(2)将上述调查的频率视为概率,从该网站所有会员(数量最多)的“小排量汽车”和“大排量汽车”中分别抽出2辆,记X表示抽取的4辆中加95号汽油的车辆数,求X的分布列和期望.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| 加油类型 汽车排量 | 小排量 | 大排量 |
| 92号 | 160 | 96 |
| 95号 | 20 | 24 |
(2)将上述调查的频率视为概率,从该网站所有会员(数量最多)的“小排量汽车”和“大排量汽车”中分别抽出2辆,记X表示抽取的4辆中加95号汽油的车辆数,求X的分布列和期望.
11.下列函数中,为偶函数的是( )
| A. | $y=\sqrt{x}$ | B. | y=2x | C. | y=sinx | D. | y=cosx |