题目内容
已知曲线C1的参数方程为
(t为参数),曲线C2的极坐标方程为ρ=4sinθ,设曲线C1,C2相交于A、B两点,则|AB|的值为 .
|
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:把曲线C1的参数方程化为普通方程,曲线C2的极坐标方程化为普通方程;两方程联立,求交点弦长即可.
解答:
解:∵曲线C1的参数方程为
(t为参数),
化为普通方程是2x-y+3=0…①,
曲线C2的极坐标方程为ρ=4sinθ,
即ρ2=4ρsinθ,
化为普通方程是x2+y2=4y…②,
由①②组成方程组
,
消去y,得5x2+4x-3=0;
∴x1+x2=-
,x1x2=-
,
∵曲线C1,C2相交于A、B两点,
∴|AB|=
•
=
×
=
;
故答案为:
.
|
化为普通方程是2x-y+3=0…①,
曲线C2的极坐标方程为ρ=4sinθ,
即ρ2=4ρsinθ,
化为普通方程是x2+y2=4y…②,
由①②组成方程组
|
消去y,得5x2+4x-3=0;
∴x1+x2=-
| 4 |
| 5 |
| 3 |
| 5 |
∵曲线C1,C2相交于A、B两点,
∴|AB|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
=
| 1+22 |
(-
|
=
2
| ||
| 5 |
故答案为:
2
| ||
| 5 |
点评:本题考查了参数方程与极坐标的应用问题,解题时先把参数方程与极坐标的方程化为普通方程,再求两曲线的交点弦长,是中档题.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
阅读如图的程序框图,运行相应的程序,则输出的结果是( )


| A、6 | B、5 | C、4 | D、3 |
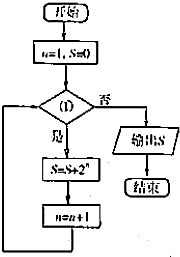 运行如图框图输出的S是254,则①应为
运行如图框图输出的S是254,则①应为 F.
F.